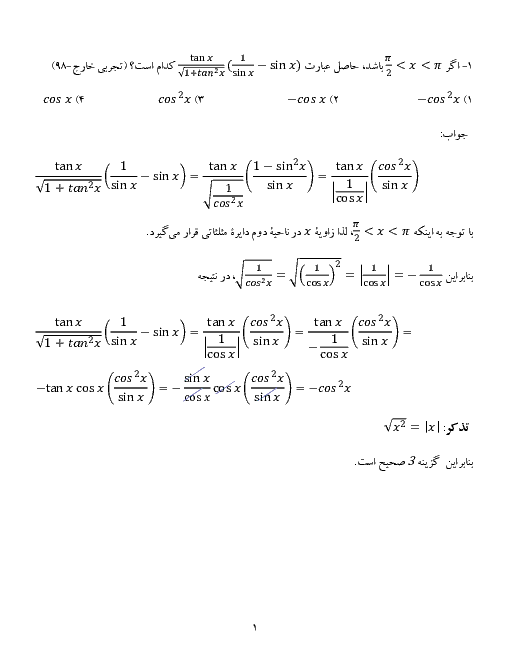
تابع $f(x)={{\operatorname{Cos}}^{2}}x+\operatorname{Sin}x$ در بازهٔ $(0,2\pi )$ در نقطه‌ای با کدام طول، اکسترمم نسبی دارد که اکسترمم مطلق نیست؟
1 )
$\frac{5\pi }{6}$
2 )
$\frac{\pi }{6}$
$\frac{\pi }{2}$
4 )
$\frac{3\pi }{2}$
پاسخ تشریحی :
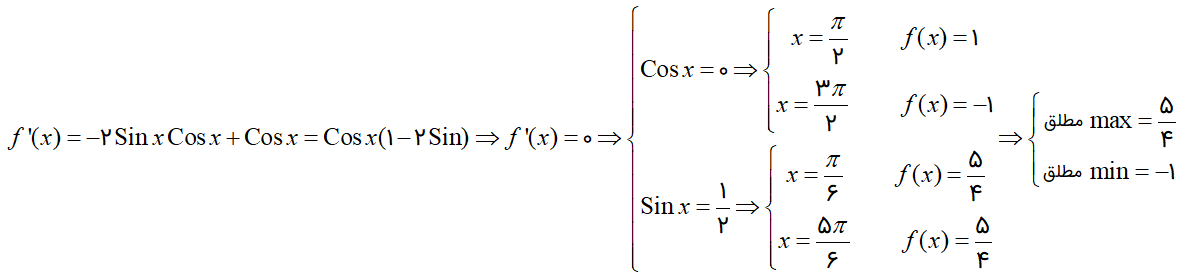
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...