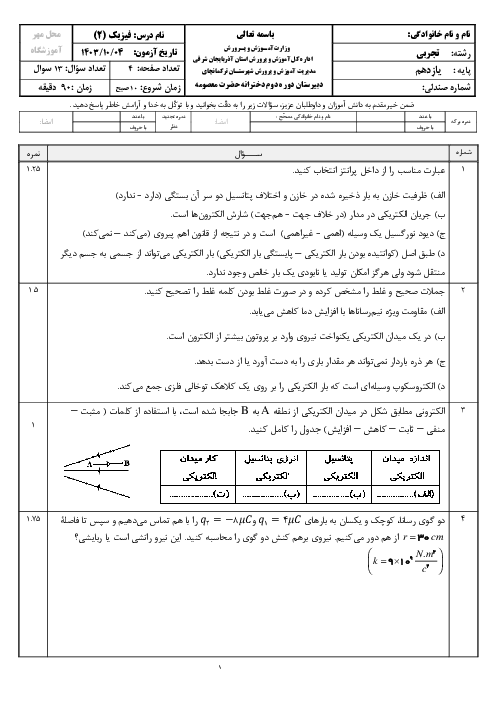
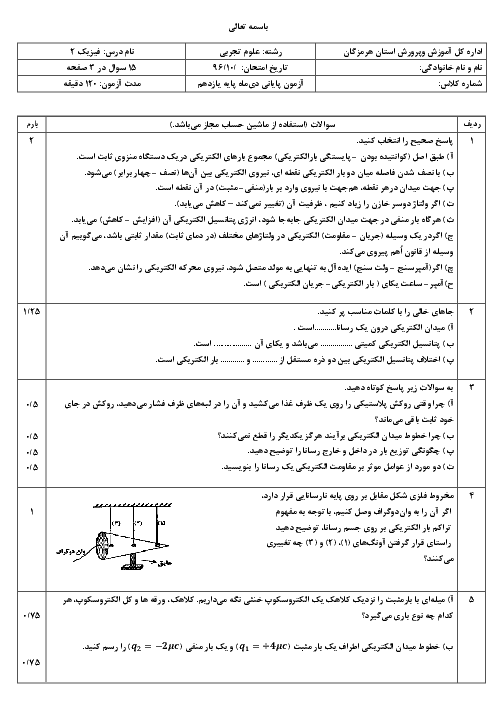
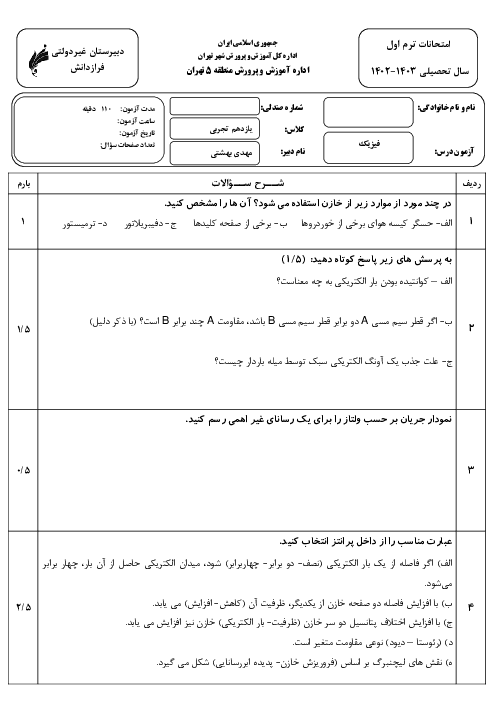
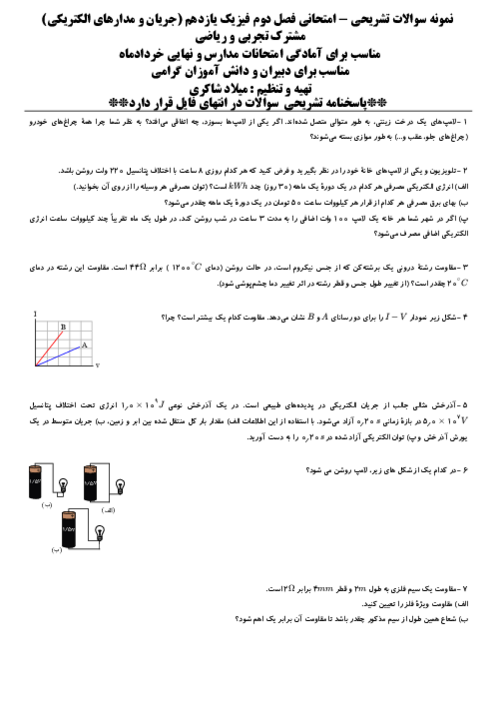چون برایند نیروهای وارد بر بار ${{q}_{4}}$ برابر با صفر اسـت، بنابراین اندازهٔ برایند نیروهای ${{\overrightarrow{F}}_{34}}$ و $({{\overrightarrow{F}}_{T}}){{\overrightarrow{F}}_{14}}$ برابر اندازهٔ نیروی ${{\overrightarrow{F}}_{24}}$ و در جهت مخالف آن میباشد. (دقت کنید دو بار ${{q}_{1}}$ و ${{q}_{3}}$ میبایست همنام و هماندازه باشند.)
با توجه به تصویر
$\left| {{\overrightarrow{F}}_{T}} \right|=\left| {{\overrightarrow{F}}_{24}} \right|$
با دو برابر شدن بارهای ${{q}_{1}}$ و ${{q}_{3}}$ جهت ${{\overrightarrow{F}}_{T}}$ تغییری نمیکند ولی اندازهٔ آن دو برابر میشود.
${{\overrightarrow{F}}^{\prime }}_{T}=2{{\overrightarrow{F}}_{T}}$
دو بردار ${{\overrightarrow{{{F}'}}}_{T}}$ و ${{\overrightarrow{F}}_{24}}$ در جهت مخالف یکدیگر هستند لذا اندازهٔ برایند آنها برابر تفاضل اندازهٔ آنهاست.
با توجه به تصویر 2
${{{F}''}_{T}}=\left| {{{{F}'}}_{T}}-{{F}_{24}} \right|=\left| 2{{F}_{T}}-{{F}_{24}} \right|={{F}_{24}}$
بنابراین
${{F}_{24}}=k\frac{\left| {{q}_{2}} \right|\left| {{q}_{4}} \right|}{r_{24}^{2}}=\frac{9\times {{10}^{9}}\times 2\times 2\times {{10}^{-12}}}{{{(3\sqrt{2}\times {{10}^{-2}})}^{2}}}=20N\Rightarrow {{F}_{24}}=20N\Rightarrow {{{F}''}_{T}}={{F}_{24}}=20N$