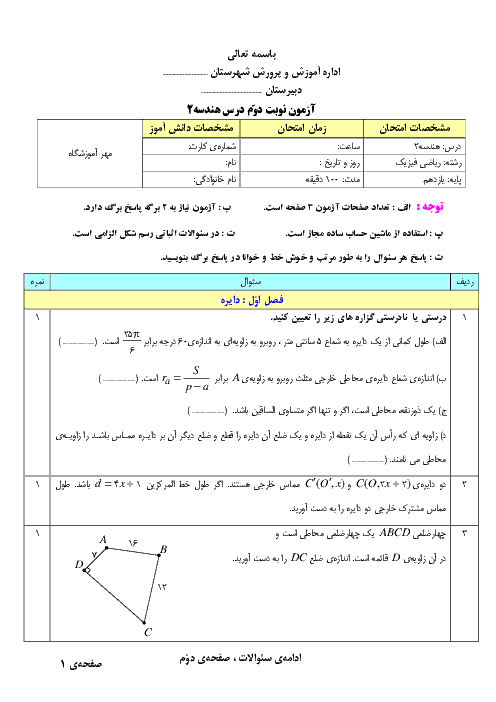
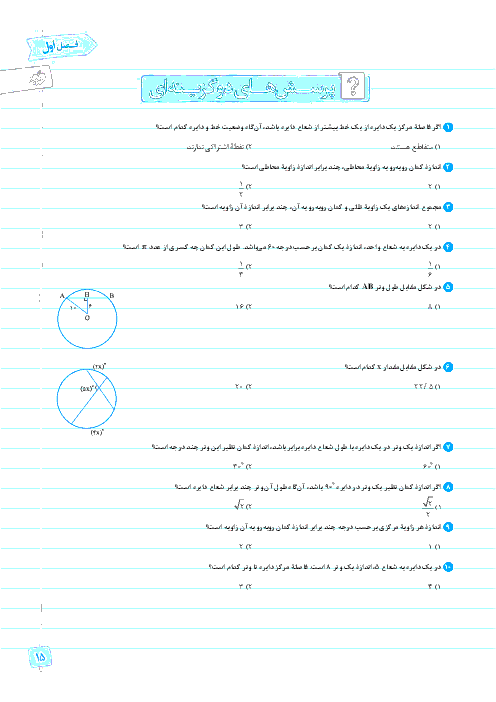
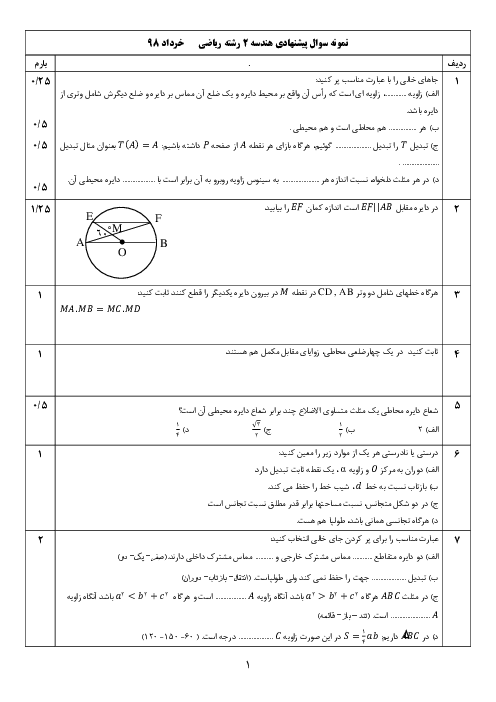
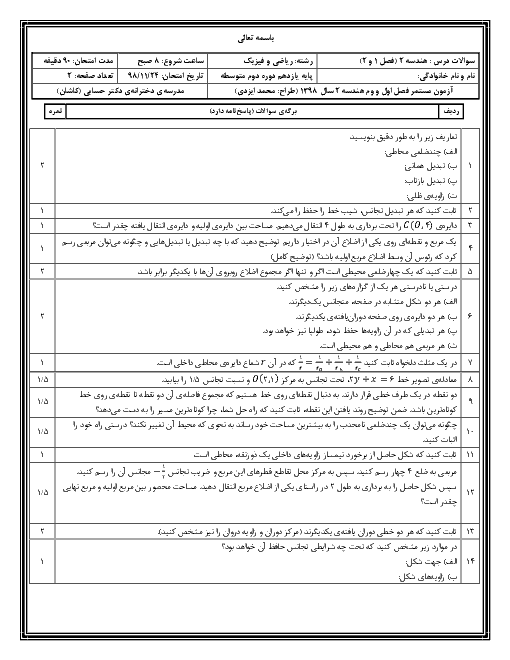
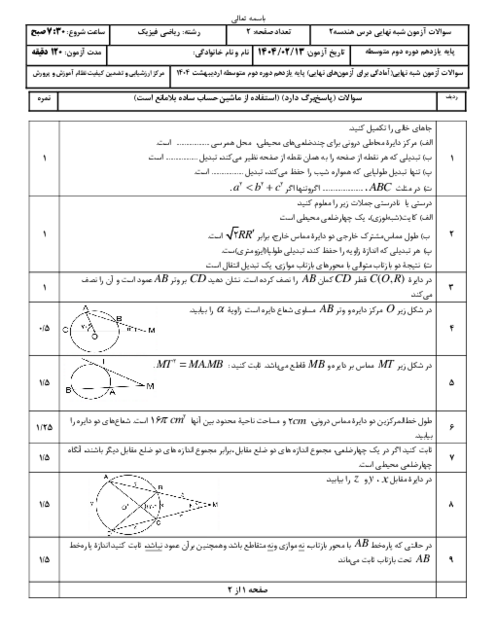درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
در مثلثی با اضلاع $a$ ،$b$ و $6$، اگر شعاع دايره‌های محاطی خارجی نظير اضلاع $a$ و $b$ را با ${{r}_{a}}$ و ${{r}_{b}}$ نشان دهيم و داشته باشيم ${{r}_{b}}=2{{r}_{a}}$، آن‌گاه $b-a$ کدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...