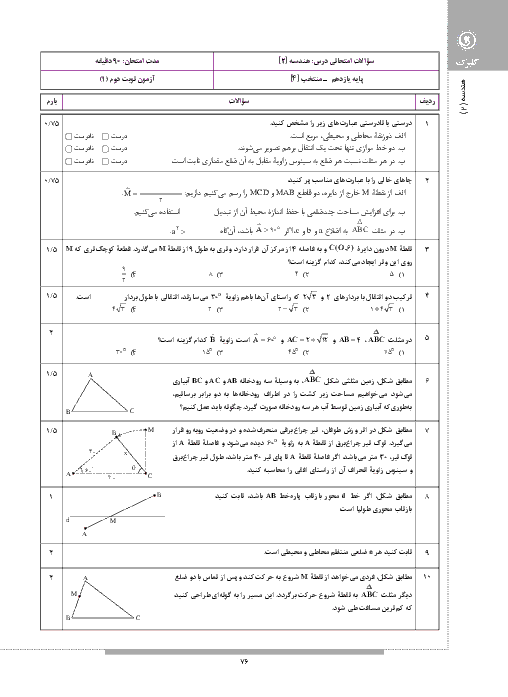
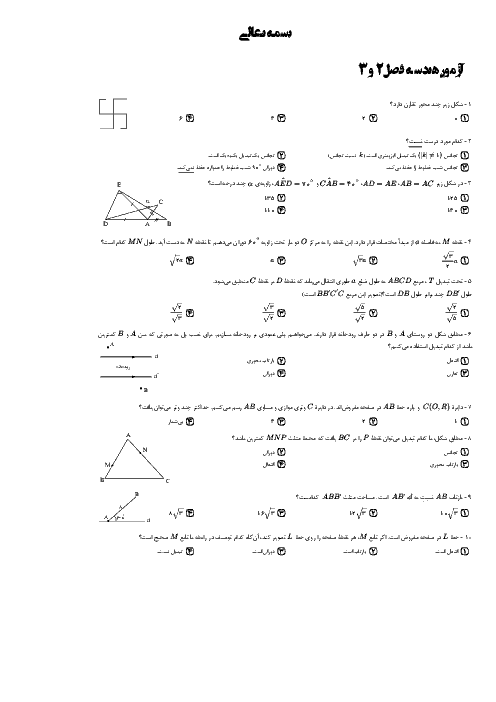
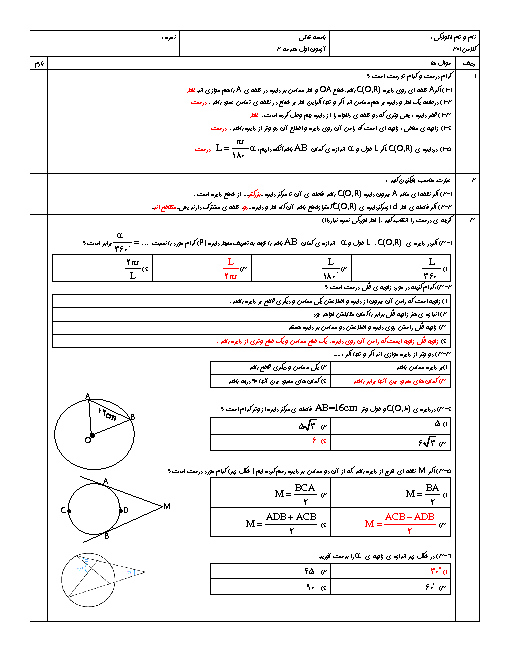
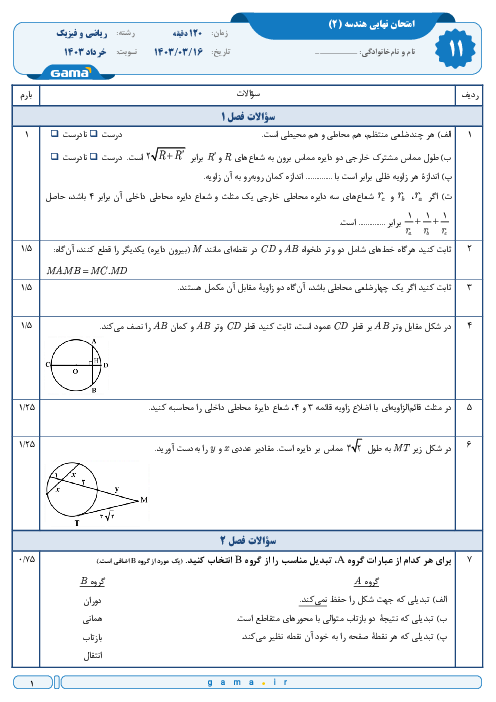
درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
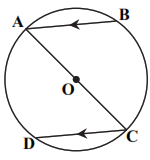
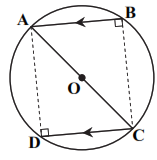
در شکل زیر AC قطر دایره است و وترهای AB و CD موازیاند. چهارضلعی ABCD همواره کدام است؟ (O مرکز دایره است.)