$\begin{align}
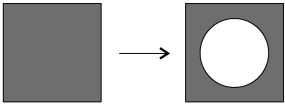
  & {{A}_{2}}={{A}_{1}}+\Delta {{A}_{1}}-{{A}_{hofre}}=425-{{A}_{hofre}} \\ 
 & \Delta {{A}_{2}}={{A}_{2}}\times 2\alpha \times \Delta {{\theta }_{2}}=(425-{{A}_{hofre}})\times 2\alpha \times 80I \\ 
 & \Delta {{A}_{2}}={{A}_{1}}\times 2\alpha \times \Delta {{\theta }_{1}}=400\times 2\alpha \times 30II \\ 
 & \Delta {{A}_{2}}=350-{{A}_{2}}=350-(425-{{A}_{hofre}})={{A}_{hofre}}-75III \\ 
 & I,II,III\Rightarrow \frac{25}{{{A}_{hofre}}-75}=\frac{400-2\alpha \times 30}{(425-{{A}_{hofre}})\times 2\alpha \times 80} \\ 
 & \Rightarrow \frac{25}{{{A}_{hofre}}-75}=\frac{5\times 30}{425-{{A}_{hofre}}}\Rightarrow 6{{A}_{hofre}}-450=425-{{A}_{hofre}} \\ 
 & \Rightarrow {{A}_{hofre}}=\frac{875}{7}=125c{{m}^{2}} \\ 
 & \frac{{{A}_{hofre}}}{{{A}_{1}}+\Delta {{A}_{1}}}=\frac{{{m}_{hofre}}}{{{m}_{kol}}}\Rightarrow \frac{125}{425}=\frac{{{m}_{hofre}}}{340} \\ 
 & \Rightarrow \frac{5}{17}=\frac{{{m}_{hofre}}}{340}\Rightarrow {{m}_{hofre}}=100g \\ 
\end{align}$