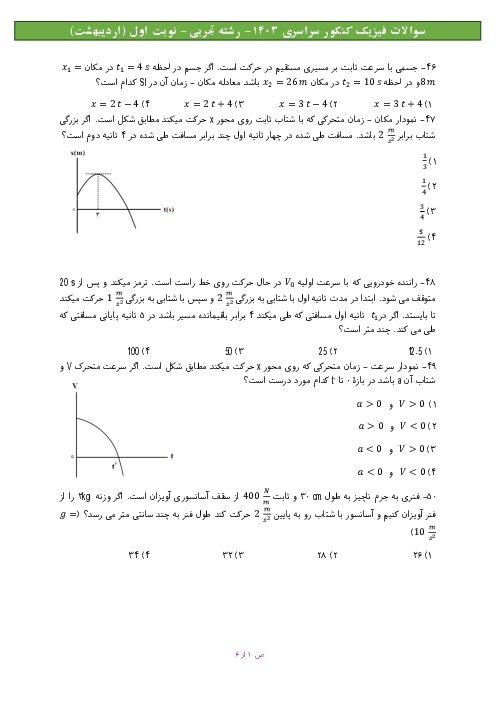
گام اول: چون متحرک در لحظهٔ $t=0$ از مبدأ مکان عبور کرده است، پس هر بار که جابجایی‌اش صفر شود، در حال عبور از مبدأ است. پس ما باید به دنبال لحظه‌هایی باشیم که جابجایی متحرک صفر شده است:

 حرکت اول $(-2m/{{s}^{2}}):\Delta {{x}_{1}}=\frac{1}{2}{{a}_{1}}{{t}^{2}}+{{v}_{{}^\circ }}t$

$\Rightarrow 0=\frac{1}{2}\times (-2){{t}^{2}}+10t\Rightarrow \left\{ \begin{matrix} {{t}_{{}^\circ }}=0 \\ {{t}_{1}}=10s \\ \end{matrix} \right.$

یعنی در لحظهٔ ${{t}_{1}}=10s$ متحرک برای دومین بار از مبدأ می‌گذرد.
گام دوم: همان‌ طور که در نمودار روبرو می‌بینید در لحظهٔ ${{t}_{1}}=10s$ شتاب حرکت هم تغییر می‌کند و حرکت دوم شروع می‌شود. از حرکت اول سرعت لحظهٔ ${{t}_{1}}=10s$ را حساب می‌کنیم تا سرعت اولیهٔ حرکت دوم را داشته باشیم:

${{v}_{1}}={{a}_{1}}{{t}_{1}}+{{v}_{{}^\circ }}=-2\times 10+10=-10m/s$

گام سوم: حالا می‌توانیم سومین عبور از مبدأ را در حرکت دوم (با شتاب $3m/{{s}^{2}}$) پیدا کنیم:

حرکت دوم $-2m/{{s}^{2}}:\Delta {{x}_{1}}=\frac{1}{2}{{a}_{1}}{{t}^{2}}+{{v}_{{}^\circ }}t$

$\Rightarrow 0=\frac{1}{2}\times (-2){{t}^{2}}+10t\Rightarrow \left\{ \begin{matrix} {{t}_{{}^\circ }}=0 \\ {{t}_{1}}=10s \\ \end{matrix} \right.$

یعنی در لحظهٔ ${{t}_{1}}=10s$ متحرک برای دومین بار از مبدأ می‌گذرد.
گام دوم: همان‌ طور که در نمودار روبرو می‌بینید در لحظهٔ ${{t}_{1}}=10s$ شتاب حرکت هم تغییر می‌کند و حرکت دوم شروع می‌شود. از حرکت 
اول سرعت لحظهٔ ${{t}_{1}}=10s$ را حساب می‌کنیم تا سرعت اولیهٔ حرکت دوم را داشته باشیم:

${{v}_{1}}={{a}_{1}}{{t}_{1}}+{{v}_{{}^\circ }}=-2\times 10+10=-10m/s$

گام سوم: حالا می‌توانیم سومین عبور از مبدأ را در حرکت دوم (با شتاب $3m/{{s}^{2}}$) پیدا کنیم:

حرکت دوم $3m/{{s}^{2}}:\Delta {{x}_{2}}=\frac{1}{2}{{a}_{2}}\Delta t_{2}^{2}+{{v}_{1}}\Delta {{t}_{2}}$

$\Rightarrow 0=\frac{1}{2}\times 3\times \Delta t_{2}^{2}+(-10)\Delta {{t}_{2}}$

$\Rightarrow \left\{ \begin{matrix} \Delta {{t}_{2}}=0 \\ \Delta {{t}_{2}}=\frac{20}{3}s \\ \end{matrix} \right.\Rightarrow {{t}_{2}}=10+\frac{20}{3}=\frac{50}{3}s$