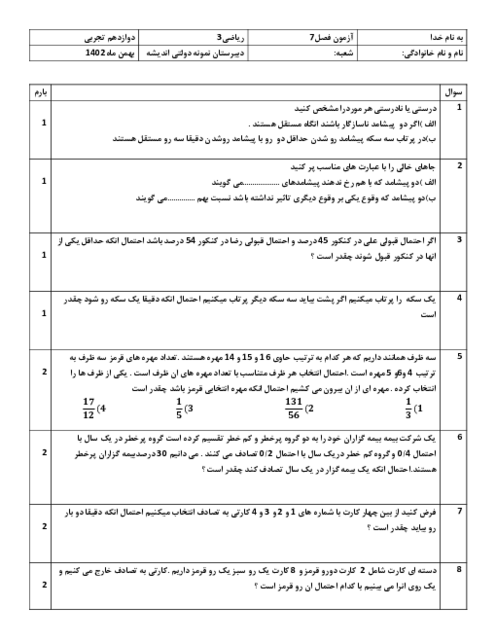
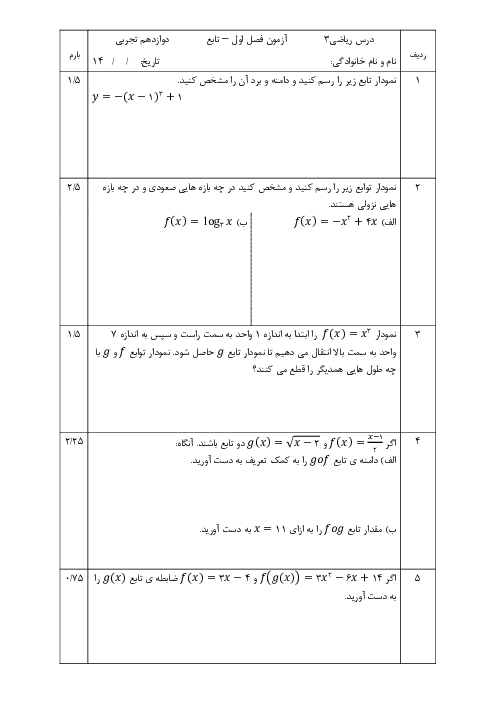
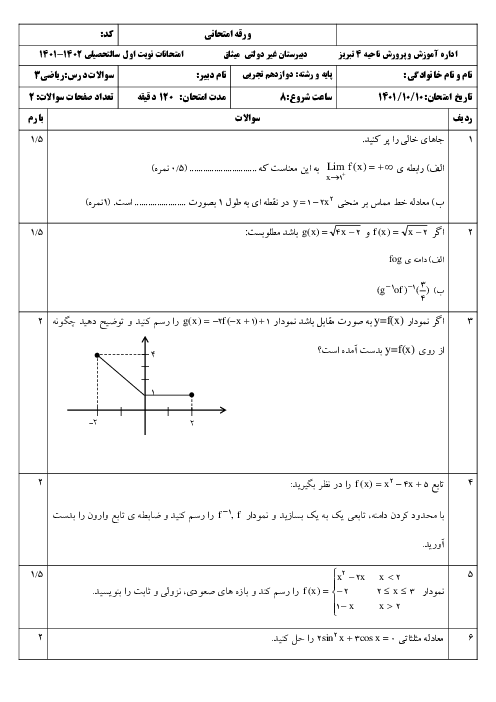
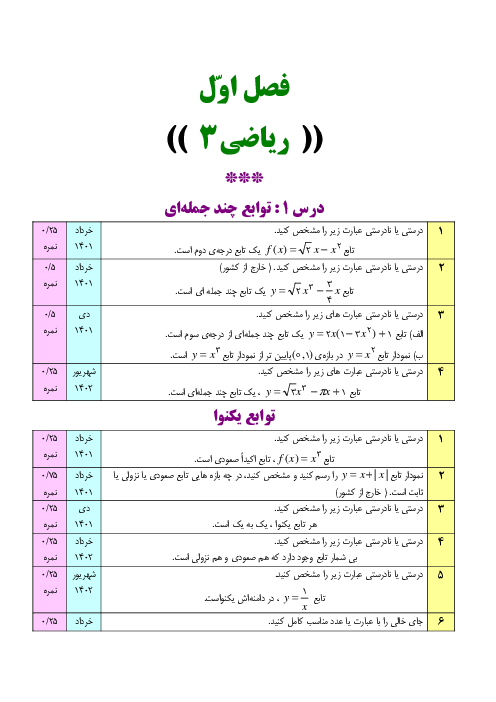
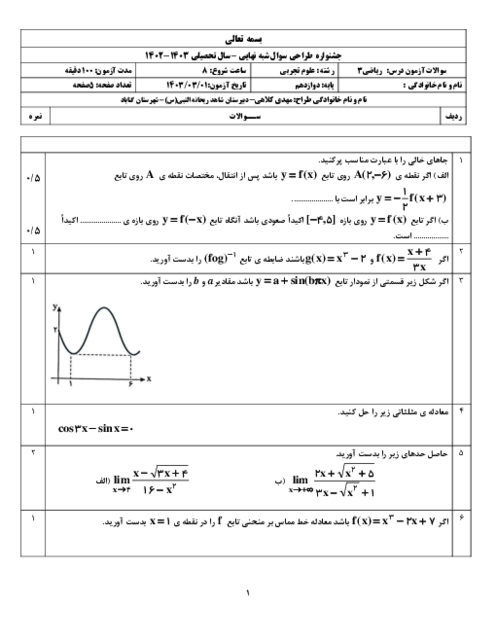
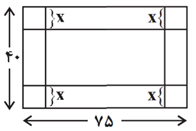
مطابق شکل زیر می‌خواهیم با برش زدن مربع‌هایی با اندازه‌های مساوی از چهار گوشهٔ یک قطعه مقوای $40\times 75$ سانتی‌متر، یک جعبهٔ در باز بسازیم. طول ضلع مربع‌های جدا شده باید چه‌قدر باشد تا حجم جعبه، بیش‌ترین مقدار ممکن را داشته باشد؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...