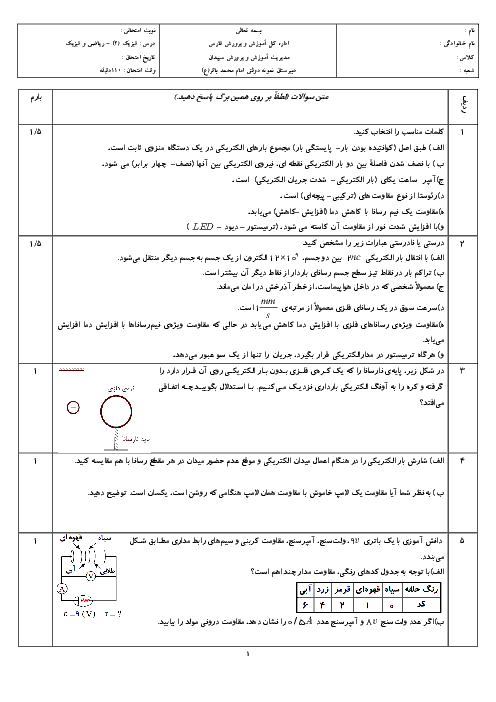
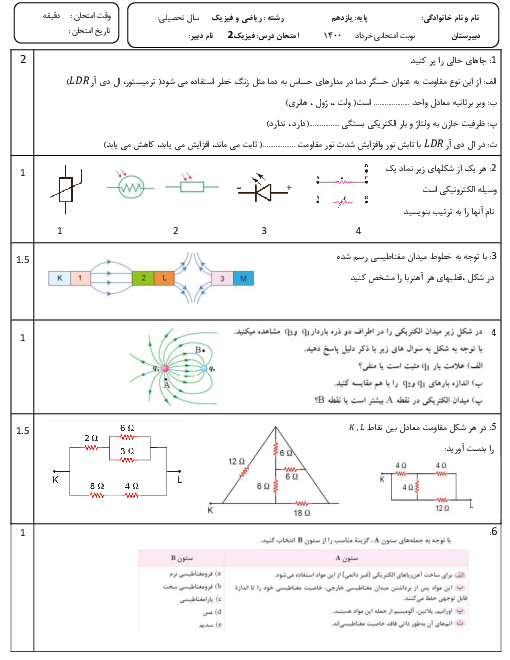
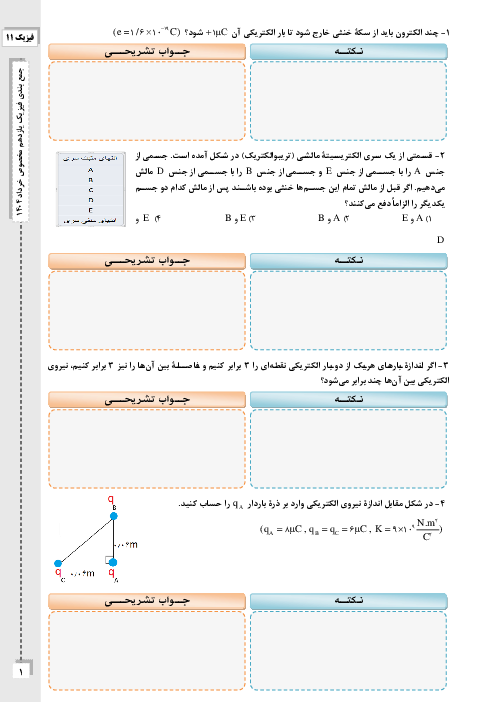
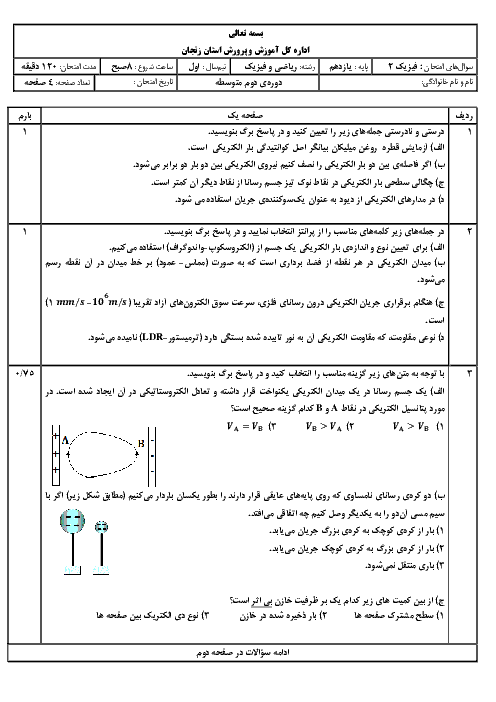
قبل از هر چیز می‌دانیم که چون هر سه بار در حال تعادل‌اند، ${{q}_{2}}\lt 0$ است. از طرف دیگر بدیهی است که میدان الکتریکی ناشی از بار ${{q}_{3}}$ در نقطهٔ A ، از میدان الکتریکی ناشی از بار ${{q}_{1}}$ در نقطهٔ A بزرگ‌تر است.

$\begin{matrix}    {{E}_{3}}=\frac{k\left| {{q}_{3}} \right|}{r_{3}^{2}}=k\times \frac{8\times {{10}^{-9}}}{{{6}^{2}}\times {{10}^{-4}}}=k\frac{2}{9}\times {{10}^{-5}}  \\    {{E}_{1}}=\frac{k\left| {{q}_{1}} \right|}{r_{1}^{2}}=k\times \frac{2\times {{10}^{-9}}}{{{12}^{2}}\times {{10}^{-4}}}=k\frac{1}{72}\times {{10}^{-5}}  \\ \end{matrix}\Rightarrow {{E}_{3}}\gt {{E}_{1}}$

حال برای تعیین جهت میدان الکتریکی در نقطهٔ A (چون 3 بار الکتریکی در اطراف A هستند)، جهت میدان‌های الکتریکی ناشی از بارهای ${{q}_{1}}$، ${{q}_{2}}$ و ${{q}_{3}}$ را می‌یابیم.
با توجه به تصویر
بدیهی است که چون ${{E}_{3}}+{{E}_{2}}\gt {{E}_{1}}$ است، بردار برایند میدان‌های الکتریکی در نقطهٔ A در جهت منفی محور x است.