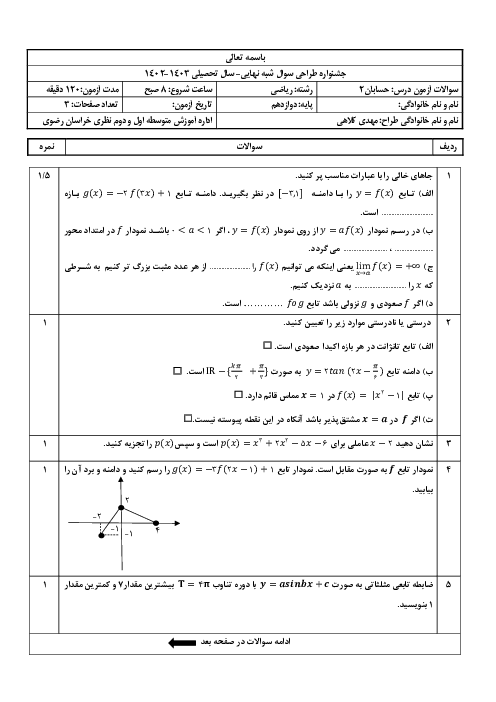
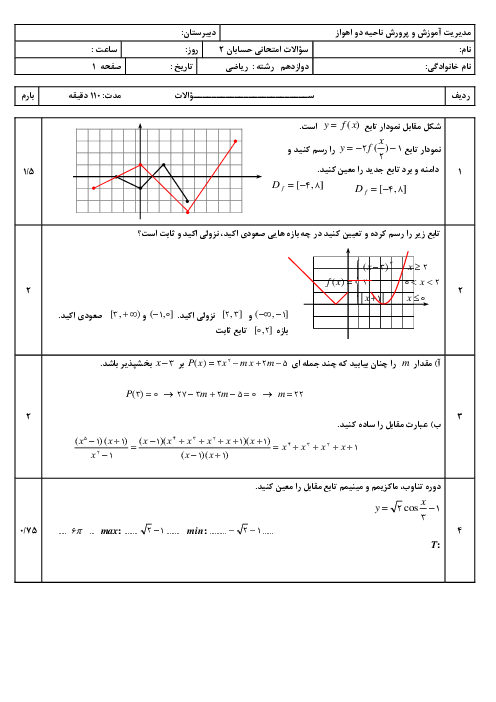
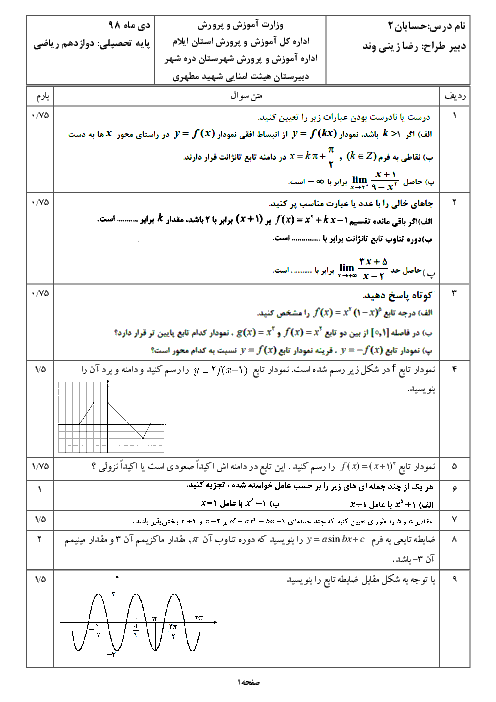
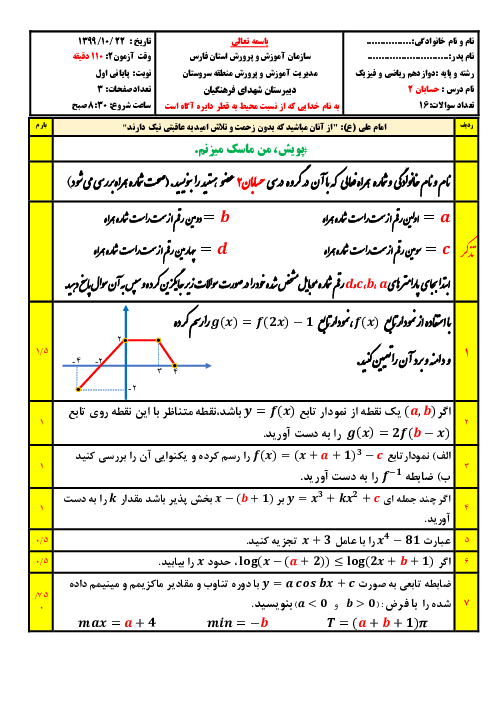
نكته: تابع f در يک بازه اكيداً نزولی میگوييم اگر برای هر دو مقدار $a$ و $b$ در اين بازه كه $a\lt b$، آنگاه $f(a)\gt f(b)$. در فاصلهای كه يک تابع اكيداً نزولی است، با حركت روی نمودار (از چپ به راست)، همواره به پايين خواهيم رفت.
تابع $y={{(\frac{1}{2})}^{x}}$ يک تابع اكيداً نزولی است، زيرا نمودار آن بهشكل زير است. پس اگر قرار باشد نمودار $f(x)$ بالاتر از $f(\frac{1}{x})$ باشد، داریم:
$f(x)\gt f(\frac{1}{x})\xrightarrow{f}x\lt \frac{1}{x}$
با توجه به علامت $x$ داريم:
$\left\{ \begin{matrix} x\gt 0:{{x}^{2}}\lt 1\Rightarrow -1\lt x\lt 1\to 0\lt x\lt 1 \\ x\lt 0:x\lt \frac{1}{x}\Rightarrow {{x}^{2}}\gt 1\Rightarrow \left\{ \begin{matrix} x\gt 1 \\ x\lt -1 \\ \end{matrix}\to x\lt -1 \right. \\ \end{matrix} \right.$
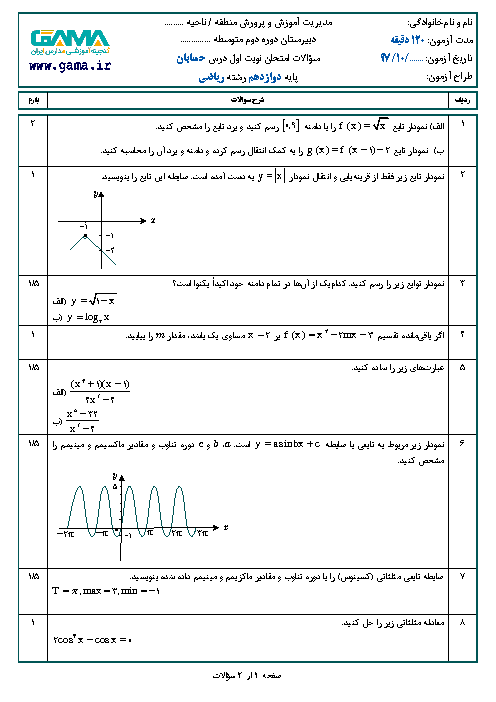
بنابراين جواب نهايی بهصورت $(-\infty ,-1)\bigcup (0,1)$ است.