** فصل 3: حد بی‌نهایت و حد در بی‌نهایت
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
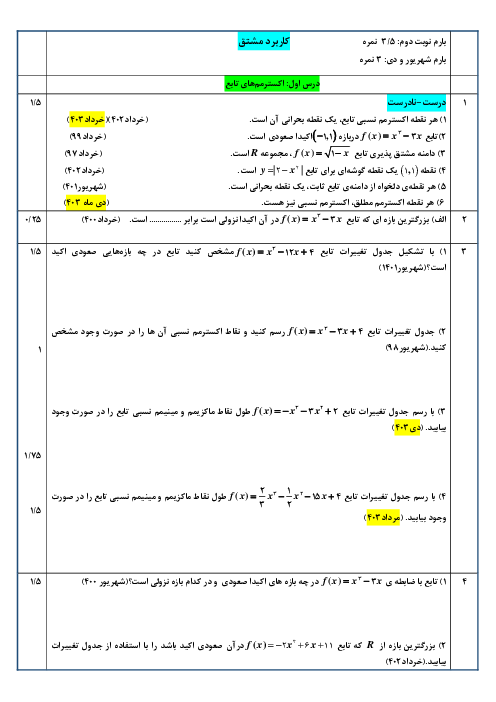
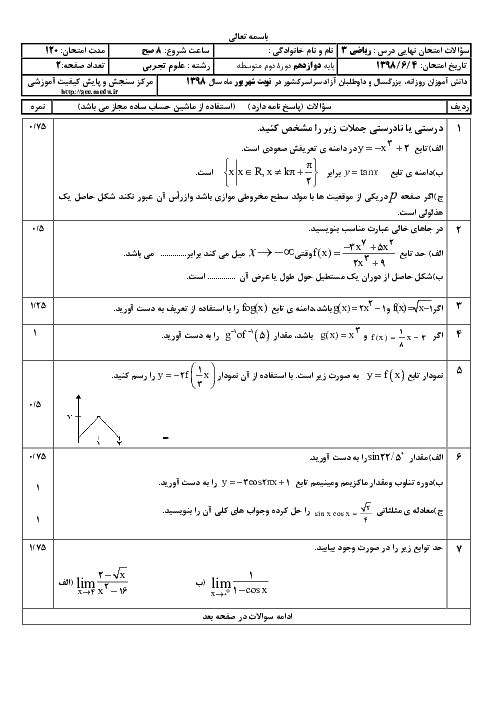
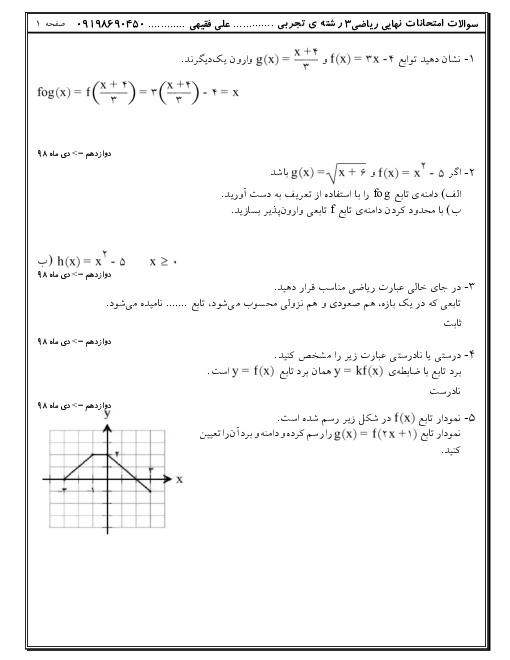
حد توابع زیر را در صورت وجود محاسبه کنید.
الف) $\mathop {\lim }\limits_{x \to 5} \frac{{2 - \sqrt {x - 1} }}{{x - 5}}$
ب) $\mathop {\lim }\limits_{x \to ( - \frac{1}{3})} \frac{{\left[ x \right]}}{{\left| {3x + 1} \right|}}$
ج) $\mathop {\lim }\limits_{x \to + \infty } \frac{{3 + \frac{1}{{{x^2}}}}}{{\frac{4}{x} - 5}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
هاشم مروانی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...