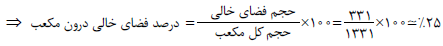حجم هر اتم کروی را میتوانیم از رابطهٔ زیر به دست آوریم:
${{V}_{atom}}=\frac{4}{3}\pi {{r}^{3}}=\frac{4}{3}\times 3\times {{(0/5\times {{10}^{-10}})}^{3}}=0/5\times {{10}^{-30}}{{m}^{3}}$
حجم یک اتم $\times $ تعداد اتمها = فضای اشغال شده توسط اتمها
$=(2\times {{10}^{27}})\times (0/5\times {{10}^{-30}})={{10}^{-3}}{{m}^{3}}={{10}^{3}}c{{m}^{3}}$
حجم مکعب = $V={{a}^{3}}={{(11)}^{3}}=1331c{{m}^{3}}$
حجم فضای خالی درون مکعب را میتوان از رابطهٔ زیر به دست آورد:
سانتیمترمکعب 331= 1331-1000 = حجم اتمها - حجم مکعب = حجم فضای خالی درون مکعب