در شکل زیر نمودار توابع خطی f و g رسم شده است؛ ضابطهٔ تابع g کدام است؟ | ریاضی و آمار (1) دهم شماره 245834 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم نمونه سوال گام به گام سوالات امتحان نهایی کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 3: نمودار تابع خطی ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

در شکل زیر نمودار توابع خطی f و g رسم شده است؛ ضابطهٔ تابع g کدام است؟

1 )

$g(x) = \frac{8}{5}x + \frac{8}{5}$

2 )

$g(x) = \frac{4}{5}x + \frac{2}{5}$

3 )

$g(x) = \frac{4}{5}x + \frac{4}{5}$

4 )

$g(x) = \frac{8}{5}x + \frac{4}{5}$

نمایش پاسخ

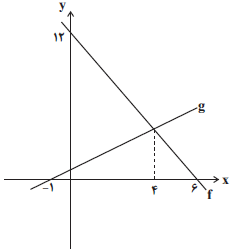
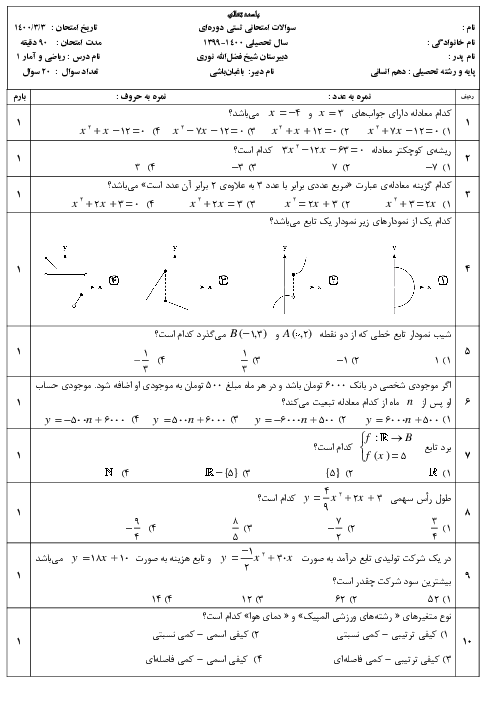
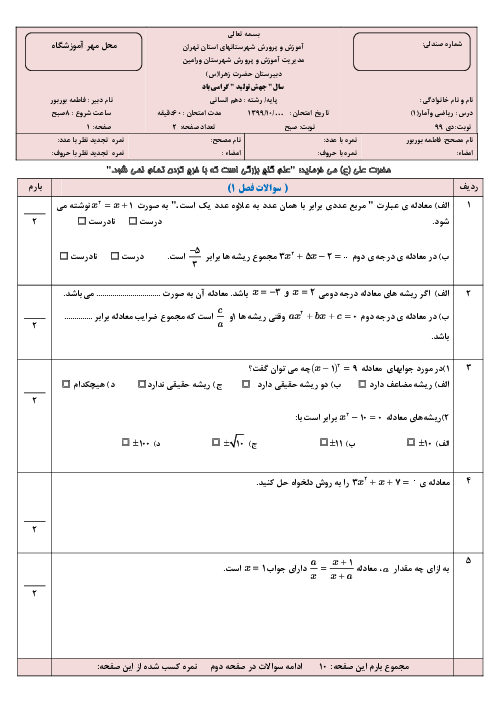
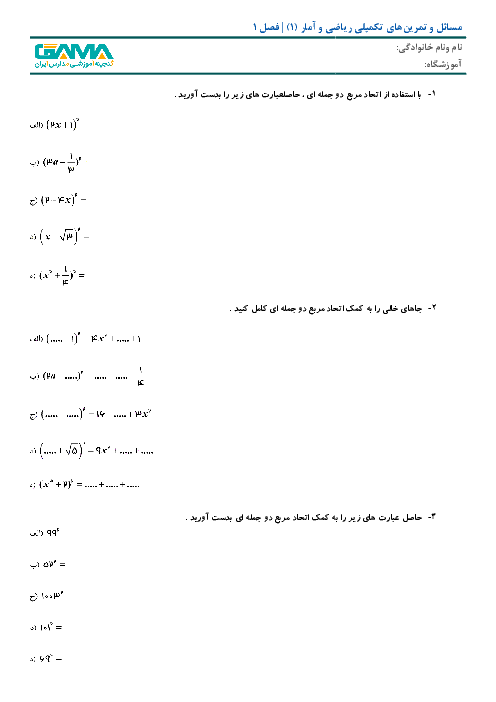
با توجه به نمودار تابع $f$ که از دو نقطهٔ $A(6,0)$ و $B(0,12)$ می‌گذرد ابتدا ضابطهٔ آن را می‌یابیم:

${}^mAB = \frac{{{}^yB - {}^yA}}{{{}^xB - {}^xA}} \Rightarrow {}^mAB = \frac{{12 - 0}}{{0 - 6}} = \frac{{12}}{{ - 6}} = - 2$

${}^{y - y}A = {}^mAB = ({}^{x - x}A) \Rightarrow y - 0 = - 2(x - 6)$

$ \Rightarrow y = - 2x + 12 \Rightarrow f(x) = - 2x + 12$

حال با جایگذاری $x = 4$ در ضابطهٔ $f$ مقدار آن را می‌یابیم:

$f(x) = - 2 \times (4) + 12 = - 8 + 12 = 4$

پس نمودار تابع $g$ از دو نقطهٔ $M(4,4)$ و $N( - 1,0)$ می‌گذرد، داریم:

${}^mMN = \frac{{{}^yM - {}^yN}}{{{}^xM - {}^yN}} \Rightarrow {}^mMN = \frac{{4 - 0}}{{4 - ( - 1)}} = \frac{4}{5}$

${}^{y - y}N = {}^mMN({}^{x - x}N)$

$ \Rightarrow y - 0 = \frac{4}{5}(x - ( - 1)) \Rightarrow y = \frac{4}{5}x + \frac{4}{5}$

$g(x) = \frac{4}{5}x + \frac{4}{5}$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

تحلیل ویدئویی برای این تست ثبت نشده است!

ویدیو دوره آموزشی، ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری

مدرس: مجتبی خالقی

مدت دوره: 7 ساعت (12 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

امتحان ترم اول ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه دانشجو | دی 98

3 صفحه

امتحان ترم اول ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه دانشجو | دی…

امتحان دهمی ها

رایـــــگان

آزمون تکوینی ریاضی و آمار (1) پایه دهم منطقه کوهمره | اسفند 96: فصل 1 تا 3

2 صفحه

آزمون تکوینی ریاضی و آمار (1) پایه دهم منطقه کوهمره | اسفند 96: فصل 1…

سعید شریفی

رایـــــگان

سوالات امتحانات ترم اول ریاضی و آمار دهم انسانی مدارس سرای دانش | دی 98

8 صفحه

سوالات امتحانات ترم اول ریاضی و آمار دهم انسانی مدارس سرای دانش | دی 98

سرای دانش

جزوه آموزشی ریاضی و آمار (1) دهم انسانی | نمودارهای چند متغیره (نمودار راداری و حبابی)

8 صفحه

جزوه آموزشی ریاضی و آمار (1) دهم انسانی | نمودارهای چند متغیره (نمودار…

سکینه باقری فرد

گام به گام ریاضی و آمار (1) پایه دهم رشته انسانی و معارف | فصل 2: معادلۀ درجه دوم

24 صفحه

گام به گام ریاضی و آمار (1) پایه دهم رشته انسانی و معارف | فصل 2: معادلۀ…

گام به گام دهم

امتحان نوبت اول رياضی و آمار (1) دهم رشته ادبیات و علوم انسانی دبیرستان امام خمینی بند پی شرقی | دی 96

1 صفحه

امتحان نوبت اول رياضی و آمار (1) دهم رشته ادبیات و علوم انسانی دبیرستان…

اسماعیل ادبی فیروزجایی

آزمون حل مسائل توصیفی و معادله درجه دو | ریاضی دهم انسانی

4 صفحه

آزمون حل مسائل توصیفی و معادله درجه دو | ریاضی دهم انسانی

فاطمه حسین پور

رایـــــگان

امتحان ریاضی و آمار 1 دهم انسانی نوبت دوم خرداد 1402 دبیرستان شهدای ایواوغلی

3 صفحه

امتحان ریاضی و آمار 1 دهم انسانی نوبت دوم خرداد 1402 دبیرستان شهدای ایواوغلی

نسیم عیوضلو

آزمون نوبت دوم ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه |‌ خرداد 1396

2 صفحه

آزمون نوبت دوم ریاضی و آمار (1) دهم انسانی دبیرستان اندیشه |‌ خرداد 1396

فاروق بختیاری نژاد

امتحان ریاضی و آمار (1) دهم دبیرستان هفده شهریور | فصل 1: معادله درجه دوم

2 صفحه

امتحان ریاضی و آمار (1) دهم دبیرستان هفده شهریور | فصل 1: معادله درجه…

فریده نوروزی

موارد بیشتر

موارد بیشتر

ارسال فایل

به ازای کدام مقدار m یکی از جواب‌های معادله 1= به توان 2 mx-x-x برابر با 4 است؟

سلام،اگر از 5 برابر عددی 4واحد کم کنیم از 3 برابر آن 2 واحد بیشتر میشود آن عدد را بیابید

دو برابر عرض مستطیلی از طول آن 3 واحد بیشتر است. اگر محیط مستطیل 120 باشد، مساحت آن؟

موارد بیشتر

ارسال پرسش

موارد بیشتر