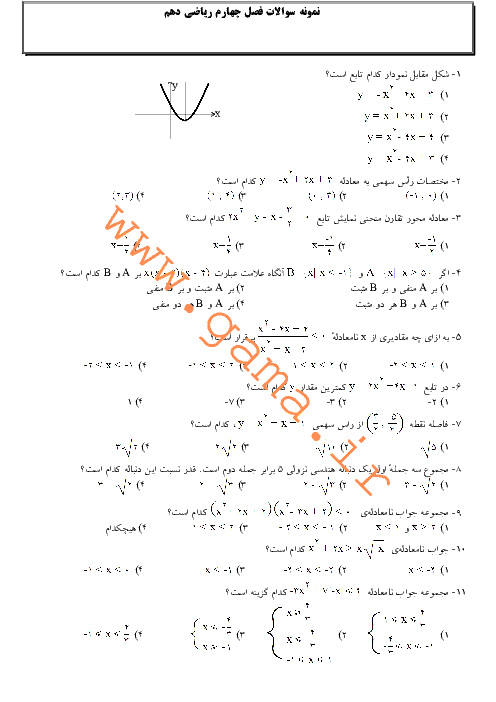
نکته: اگر $y=sin \theta$ و $x=cos \theta$، آنگاه نقطهی $P(x,y)$ روی دایرهی مثلثاتی قرار دارد و رابطهی $x^2+y^2=1$ بین $x$ و $y$ برقرار است.
نکته: اگر $\theta$ در ربع چهارم باشد، آنگاه $sin \theta \lt0$ و $cos \theta \gt0$ است.
مطابق نکات باید به دنبال نقطهای باشیم که مقدار $x$ آن مثبت و $y$ آن منفی باشد و رابطهی $x^2+y^2=1$ در آن برقرار باشد.
در گزینهی ۲، مقدار $x$ منفی است، پس نمیتواند پاسخ باشد. برای سایر گزینهها داریم:
گزینهی ۱:${{(\frac{2}{5})}^{2}}+{{(-\frac{3}{5})}^{2}}=\frac{4}{25}+\frac{9}{25}=\frac{13}{25}\ne 1$
گزینهی ۳: ${{(\frac{3}{8})}^{2}}+{{(-\frac{\sqrt{7}}{8})}^{2}}=\frac{9}{64}+\frac{7}{64}=\frac{16}{64}\ne 1$
گزینهی ۴: ${{(\frac{\sqrt{5}}{3})}^{2}}+{{(-\frac{2}{3})}^{2}}=\frac{5}{9}+\frac{4}{9}=\frac{9}{9}=1$
بنابراین گزینهی ۴ پاسخ است.