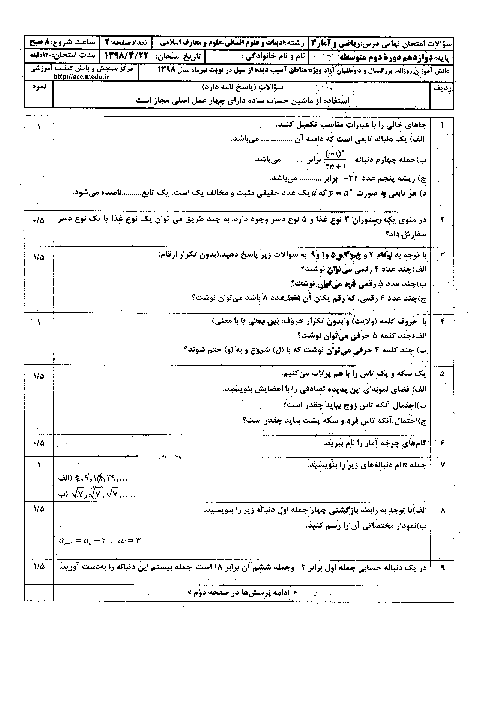
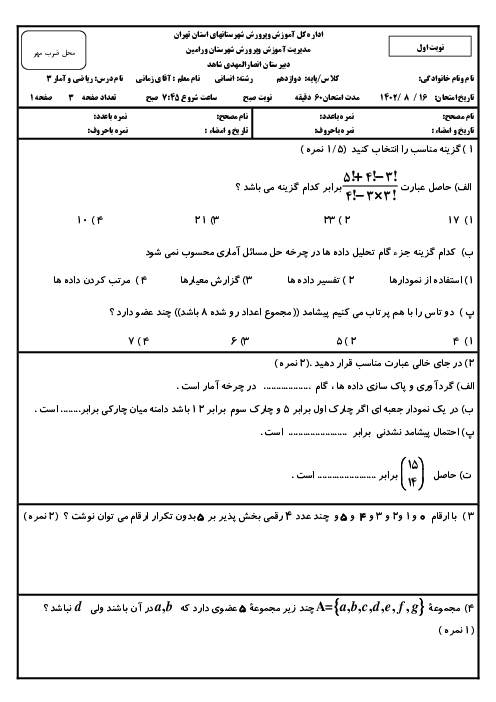
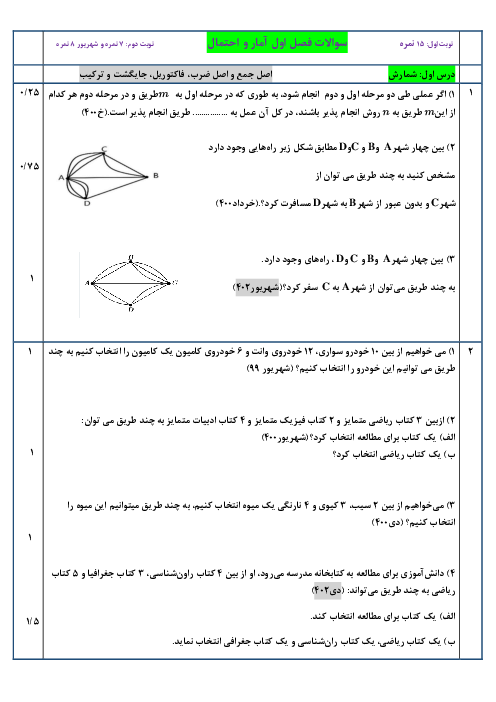
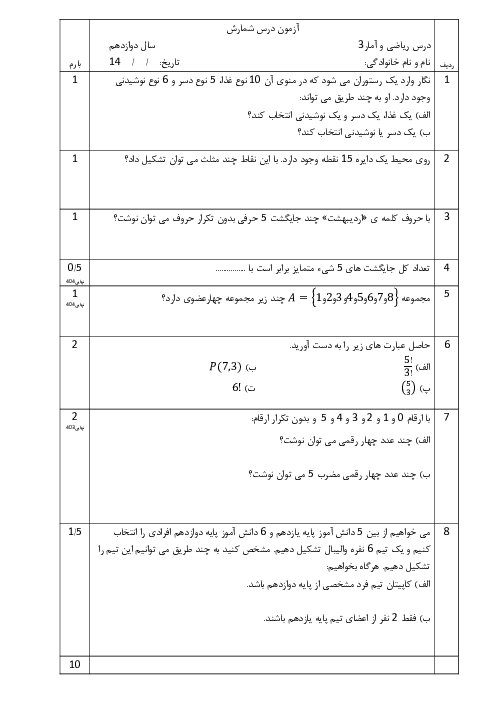
درس 3: تابع نمایی
ریاضی و آمار (3)
دوازدهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
كدام يک از گزينه‌های زير يک تابع نمايی است؟
1 )
$f\left( x \right)={{1}^{x}}$
2 )
$g\left( x \right)={{\left( -2 \right)}^{x}}$
$h\left( x \right)={{\left( \frac{\sqrt{2}}{2} \right)}^{x}}$
4 )
$t\left( x \right)={{x}^{x}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...