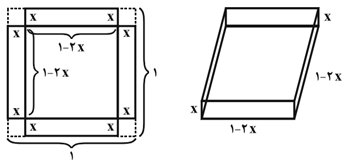
يک شيرينیفروشی میخواهد با بريدن مربعهای همنهشت از چهار گوشهٔ مقوايی مربع شكل به طول ضلع واحد و بالا بردن چهار طرف آن، جعبهای در باز بسازد. بيشترين حجم ممكن برای جعبه چند واحد مكعب است؟
1 )
$\frac{4}{9}$
$\frac{2}{27}$
3 )
$\frac{7}{15}$
4 )
$\frac{9}{31}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!