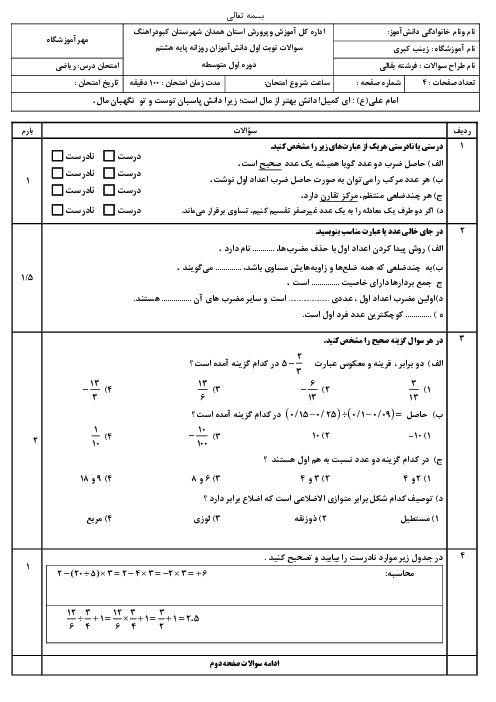
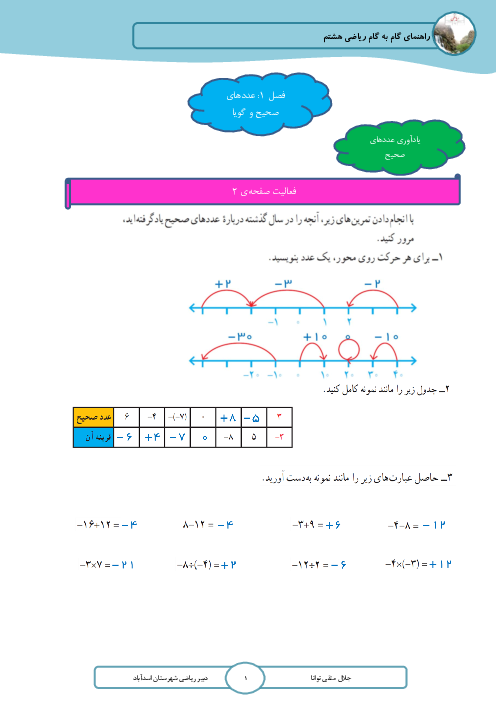
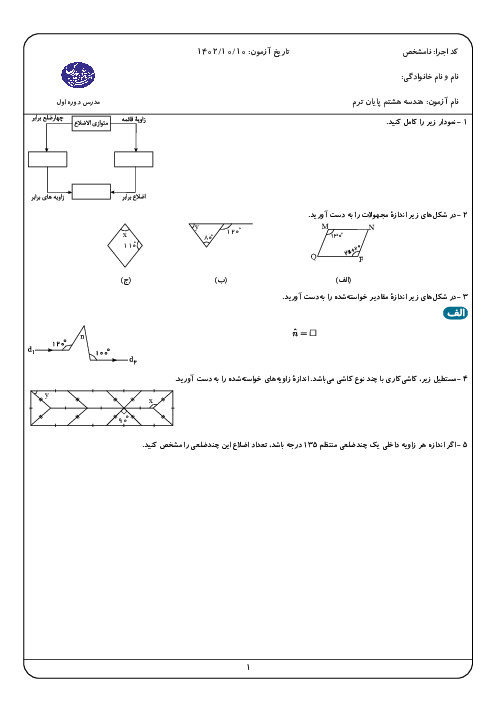
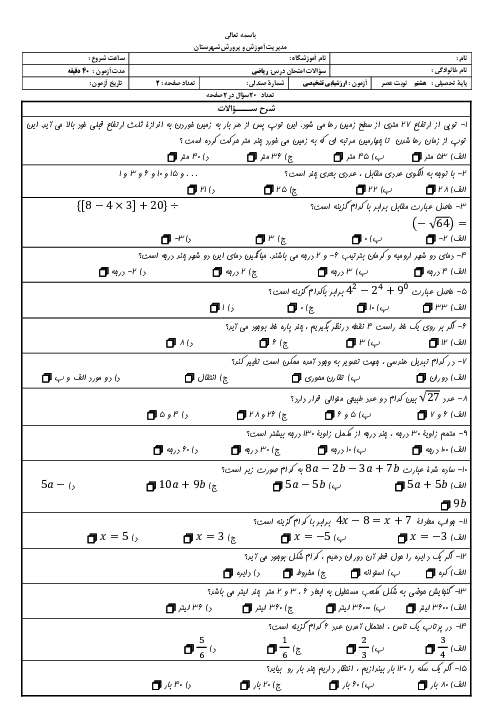
اگر $\overrightarrow{a}=\left[ \begin{matrix} 4 \\ -2 \\ \end{matrix} \right]$ و بردار $b$ سه برابر قرینهی $\overrightarrow{a}$ باشد، مختصات $\overrightarrow{x}$ کدام گزینه است؟ $-2 \overrightarrow{a}+ 2 \overrightarrow{x} =\overrightarrow{b}$
1 )
$\left[ \begin{matrix} -2 \\ -1 \\ \end{matrix} \right]$
$\left[ \begin{matrix} -2 \\ 1 \\ \end{matrix} \right]$
3 )
$\left[ \begin{matrix} 2 \\ 1 \\ \end{matrix} \right]$
4 )
$\left[ \begin{matrix} 2 \\ -1 \\ \end{matrix} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!