** فصل 5: کاربردهای مشتق
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
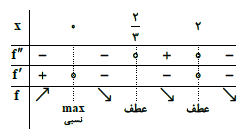
کدام گزینه در مورد نمودار تابع $f(x)=-\frac{1}{4}{{x}^{4}}+\frac{4}{3}{{x}^{3}}-2{{x}^{2}}+5$ صحیح است؟
1 )
دو ماکزیمم نسبی و یک می‌نیمم نسبی دارد.
2 )
دو می‌نیمم نسبی و یک ماکزیمم نسبی دارد.
یک ماکزیمم نسبی و دو عطف دارد.
4 )
یک می‌نیمم نسبی و دو عطف دارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...