قسمت 2: قانون القای الکترومغناطیسی فاراده
فیزیک (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
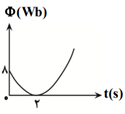
نمودار شار مغناطيسی عبوری از يک حلقه برحسب زمان بهصورت سهمی زير است. نيروی محرکهٔ القايی متوسط در دو ثانيهٔ دوم چند ولت است؟