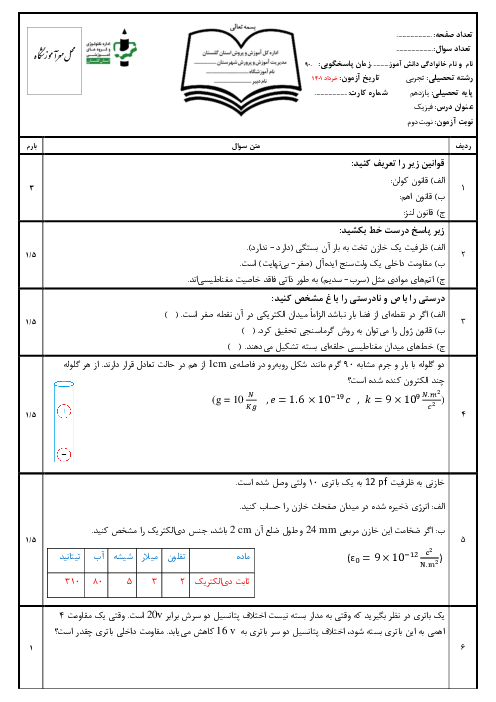
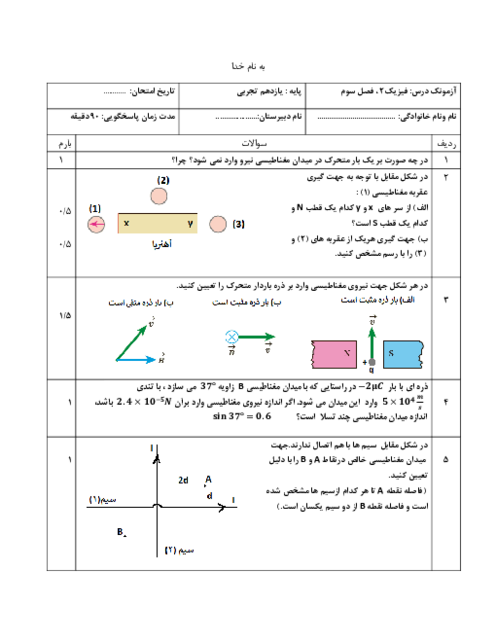
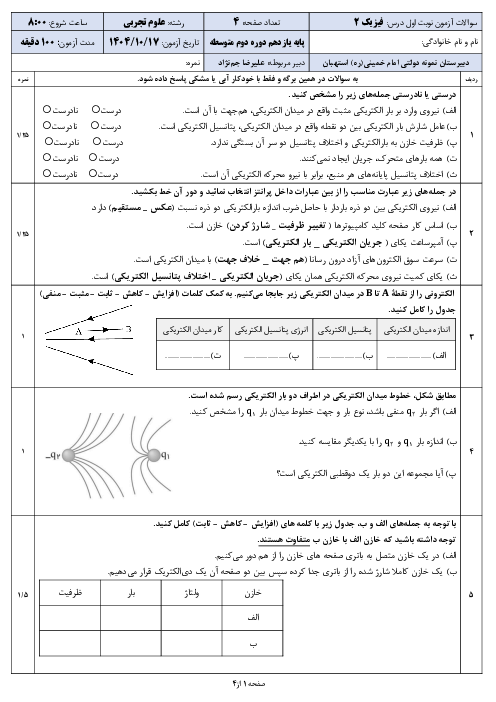
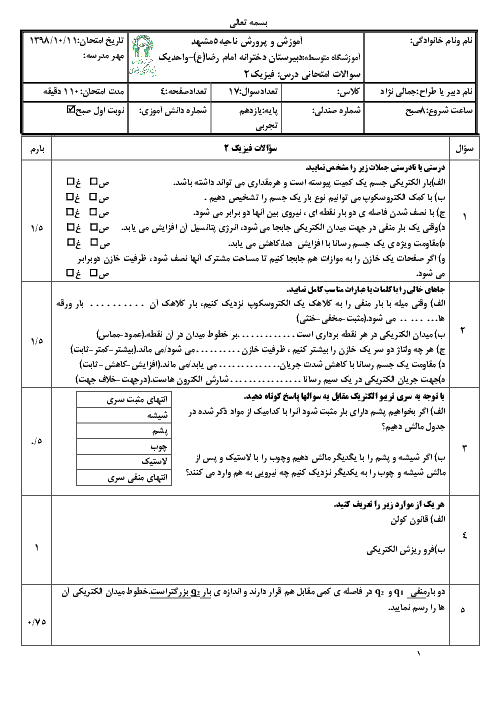
اگر بخواهيم مقاومت سيم 75 درصد كاهش يابد پس مقاومت سيم $\frac{1}{4}$ مقاومت حالت اول است.

${{R}_{2}}=\frac{1}{4}{{R}_{1}}\Rightarrow \rho \frac{{{L}_{2}}}{{{A}_{2}}}=\frac{1}{4}\rho \frac{L}{\pi {{r}^{2}}}\Rightarrow \frac{{{L}_{2}}}{{{A}_{2}}}=\frac{L}{4\pi {{r}^{2}}}$

از طرفی چون باید از داخل سیم یک استوانه با شعاع x خالی كنیم، پس سطح مقطع در حالت جدید برابر است با:

${{A}_{2}}=\pi ({{r}^{2}}-{{x}^{2}})$

$\frac{{{L}_{2}}}{\pi ({{r}^{2}}-{{x}^{2}})}=\frac{L}{4\pi {{r}^{2}}}\Rightarrow \frac{{{L}_{2}}}{L}=\frac{{{r}^{2}}-{{x}^{2}}}{4{{r}^{2}}}$

حال فرض كنيم طول ثانويهٔ سيم ${{L}_{2}}=nL$ شود، داریم:

$\frac{{{r}^{2}}-{{x}^{2}}}{4{{r}^{2}}}=n\Rightarrow {{r}^{2}}-{{x}^{2}}=4{{r}^{2}}n\Rightarrow {{x}^{2}}={{r}^{2}}(1-4n)$

$\Rightarrow x=r\sqrt{1-4n}\Rightarrow n\le \frac{1}{4}$

حال اگر $n=\frac{{{L}_{2}}}{L}=\frac{1}{8}$ باشد، در این صورت داریم:

$x=r\sqrt{1-4\times \frac{1}{8}}=r\sqrt{1-\frac{1}{2}}=\frac{\sqrt{2}}{2}r$

هنگامی كه طول آن $\frac{1}{8}$ برابر می‌شود شعاع استوانه‌ای كه خالی می‌كنيم بايد برابر $\frac{\sqrt{2}}{2}r$ باشد.

اگر $n=\frac{{{L}_{2}}}{L}=\frac{1}{6}$ باشد، داریم:

$x=r\sqrt{1-4\times \frac{1}{6}}\Rightarrow x=\frac{\sqrt{3}}{3}r$