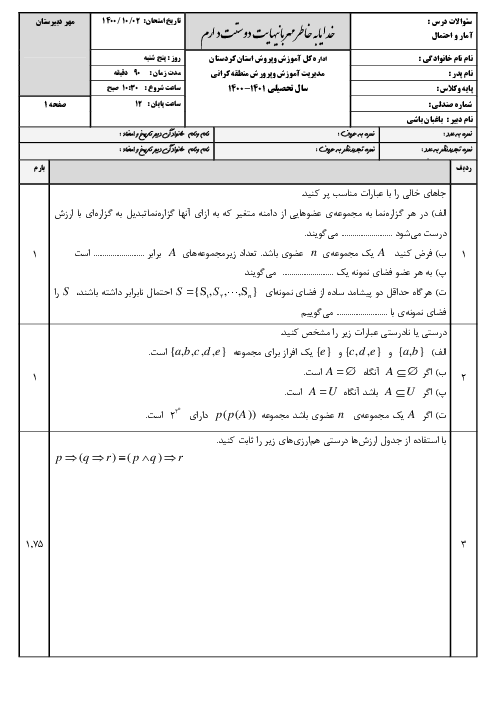
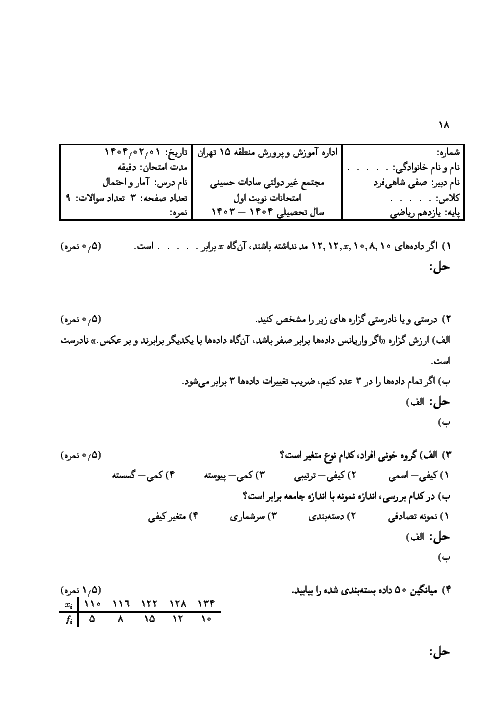
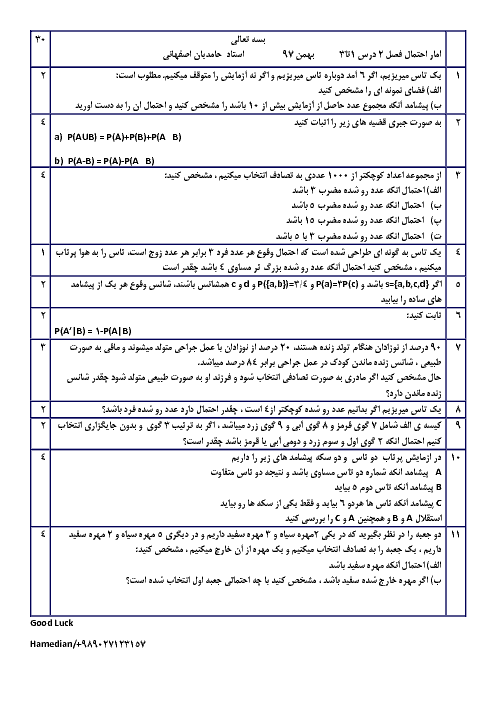
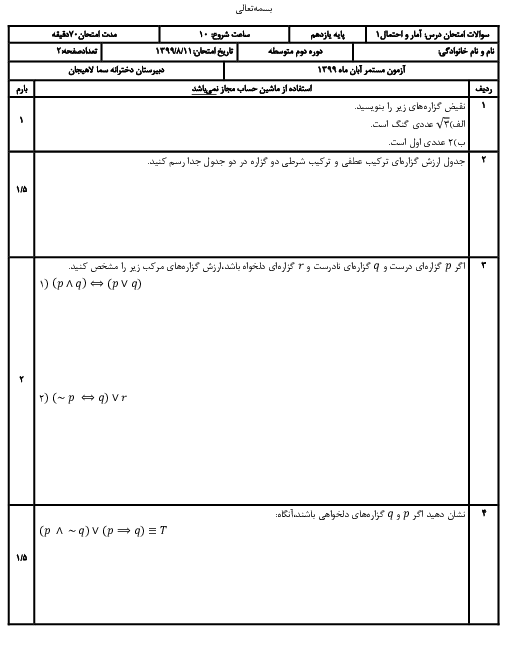
در جعبه‌ی A تعداد ۳ مهره‌ی قرمز، ۳ مهره‌ی سبز، ۱ مهره‌ی آبی و ۱ مهره‌ی زرد و در جعبه‌ی B تعداد ۴ مهره‌ی قرمز، ۴ مهره‌ی سبز و ۲ مهره‌ی آبی موجود است. اگر از هریک از جعبه‌ها تعداد یک مهره خارج کنیم، احتمال آنکه هر دو مهره هم‌رنگ باشند، کدام است؟
$\frac{۱۳}{۴۰}$
$\frac{۱۱}{۴۰}$
$\frac{۲۳}{۸۰}$
$\frac{۲۷}{۸۰}$
برای دیدن پاسخ تشریحی یک گزینه را انتخاب کن یا بزن رو