پودمان 2: تابع‌های خطی و درجۀ دوم و کاربرد آنها در حل معادله‌ها و نامعادله‌ها
ریاضی2 فنی
یازدهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
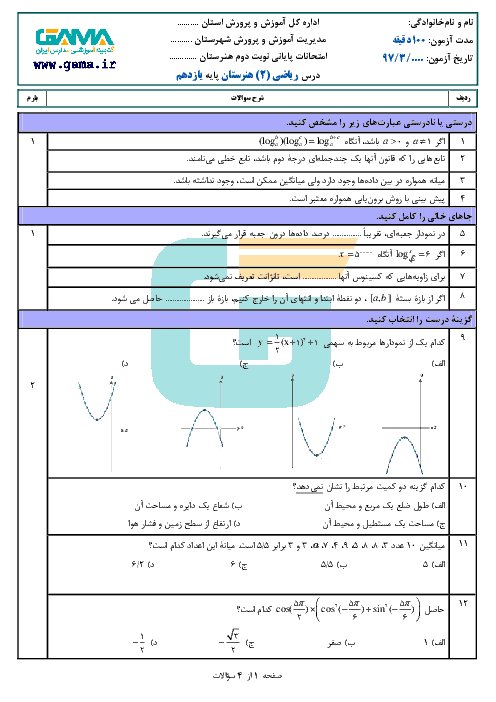
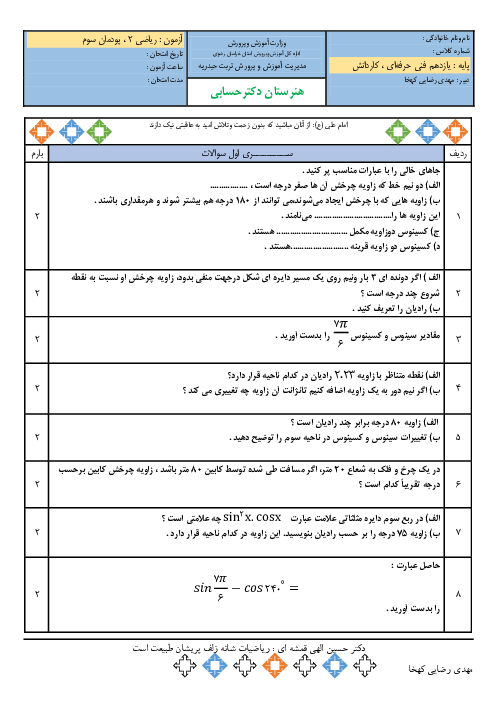
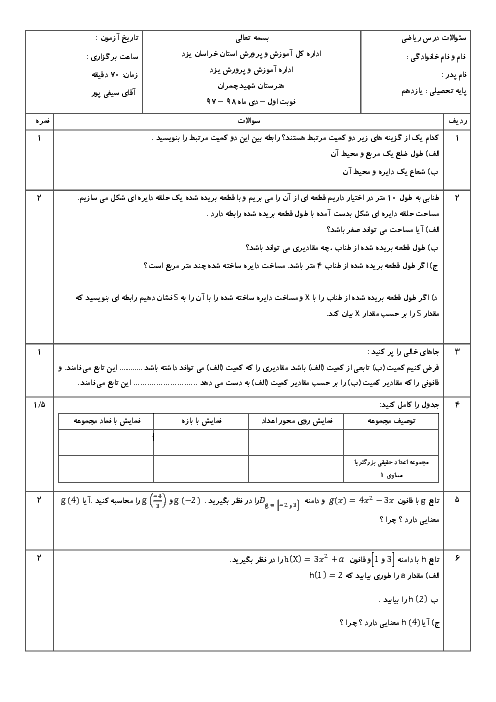
جواب نامعادله $\frac{{{x^2} - 4x}}{{2x + 1}} \le 0$ کدام است؟
1 )
$\left[ { - \frac{1}{2},0} \right] \cup \left[ {4, + \infty } \right)$
2 )
$\left( { - \frac{1}{2},0} \right] \cup \left[ {4, + \infty } \right)$
$\left( { - \infty , - \frac{1}{2}} \right] \cup \left[ {0,4} \right]$
4 )
$\left( { - \infty ,\frac{1}{2}} \right) \cup \left[ {0,4} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...