اگر ، آن‌گاه حاصل کدام است؟ | ریاضی (3) دوازدهم شماره 261939

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

موبایل یا ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

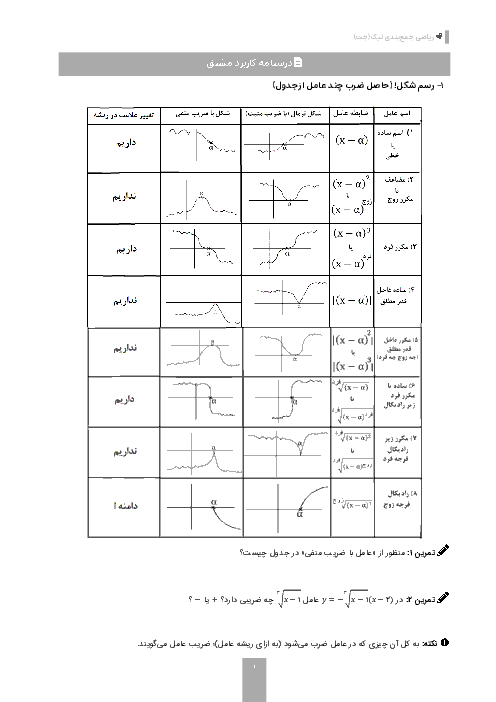
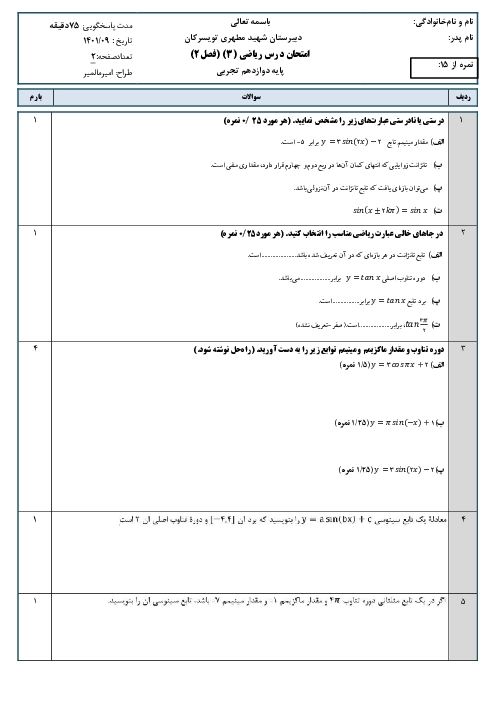
** فصل 3: حد بی‌نهایت و حد در بی‌نهایت ریاضی (3) دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

اگر $f(x)=\frac{x-\sqrt{4{{x}^{2}}+9x}}{3x+1}$، آن‌گاه حاصل $\underset{x\to +\infty }{\mathop{\lim }}\,f(x)+\underset{x\to -\infty }{\mathop{\lim }}\,f(x)$ کدام است؟

1 )

صفر

2 )

$\frac{2}{3}$

3 )

$-\frac{2}{3}$

4 )

$+\infty $

نمایش پاسخ

$f(x)=\frac{x-\sqrt{4{{x}^{2}}+9x}}{3x+1}\Rightarrow \underset{x\to \pm \infty }{\mathop{\lim }}\,f(x)=\underset{x\to \pm \infty }{\mathop{\lim }}\,\frac{x-\sqrt{4{{x}^{2}}}\left( \sqrt{1+\frac{9}{4x}} \right)}{3x+1}$

$\Rightarrow \left\{ \begin{matrix} \underset{x\to +\infty }{\mathop{\lim }}\,f(x)=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{x-2x}{3x+1}=-\frac{1}{3} \\ \underset{x\to -\infty }{\mathop{\lim }}\,f(x)=\underset{x\to -\infty }{\mathop{\lim }}\,\frac{x+2x}{3x+1}=1 \\ \end{matrix}\Rightarrow \frac{1}{3}+1=\frac{2}{3} \right.$

گزارش اشکال