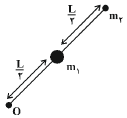
با دوران میله حول نقطهٔ $O$ به‌طور یکنواخت، دورهٔ دوران جرم‌های ${{m}_{1}}$ و ${{m}_{2}}$ يكسان است. با استفاده از رابطهٔ قانون دوم نيوتون در حركت دايره‌ای یکنواخت داریم:

$\begin{align}
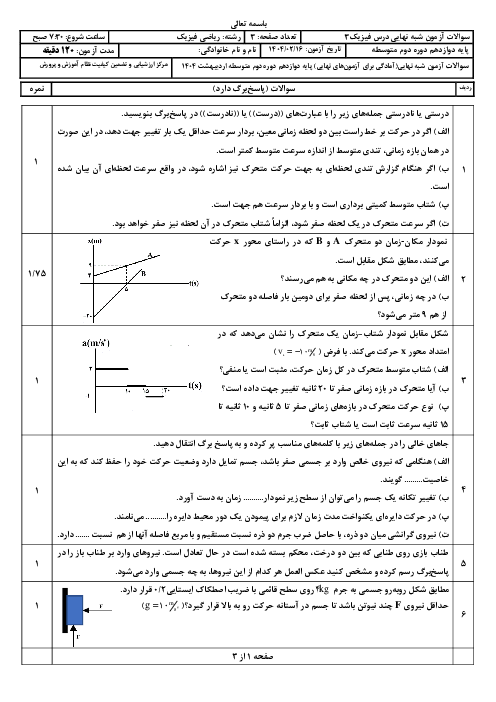
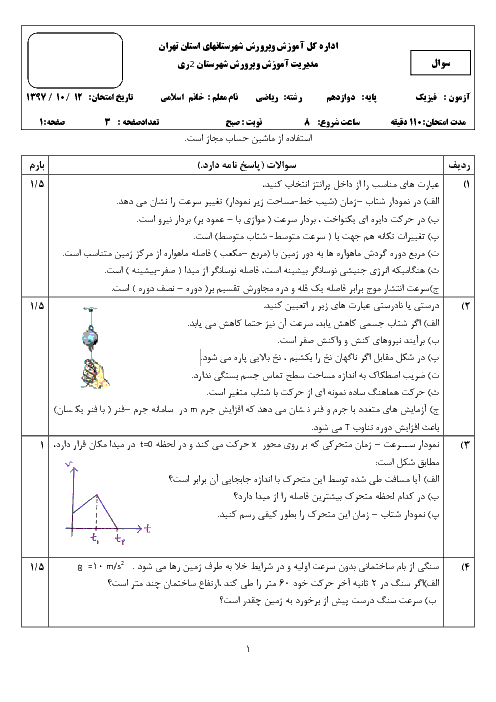
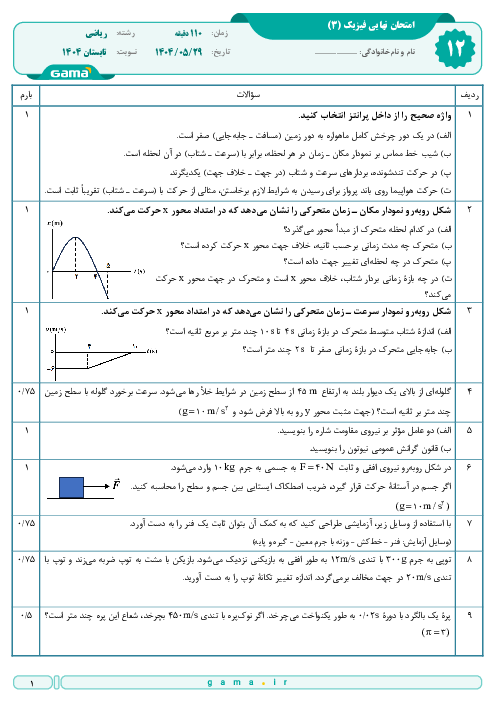
  & {{F}_{net}}=m\frac{{{v}^{2}}}{r}\xrightarrow{v=\frac{2\pi r}{T}}{{F}_{net}}=4{{\pi }^{2}}\frac{mr}{{{T}^{2}}} \\
 & \Rightarrow \frac{{{({{F}_{net}})}_{2}}}{{{({{F}_{net}})}_{1}}}=\frac{{{m}_{2}}}{{{m}_{1}}}\times \frac{{{r}_{2}}}{{{r}_{1}}}\times {{(\frac{{{T}_{1}}}{{{T}_{2}}})}^{2}} \\
 & \xrightarrow{{{T}_{1}}={{T}_{2}}}\frac{{{({{F}_{net}})}_{2}}}{{{({{F}_{net}})}_{1}}}=\frac{{{m}_{2}}}{2{{m}_{2}}}\times \frac{L}{\frac{L}{2}}\times {{1}^{2}}=1 \\
\end{align}$