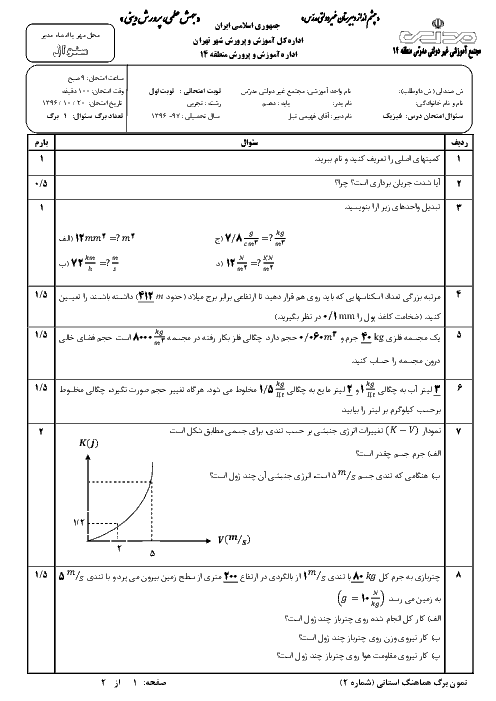
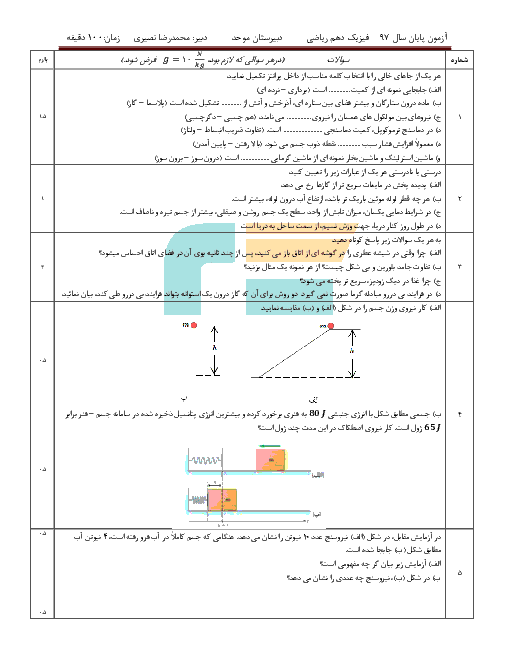
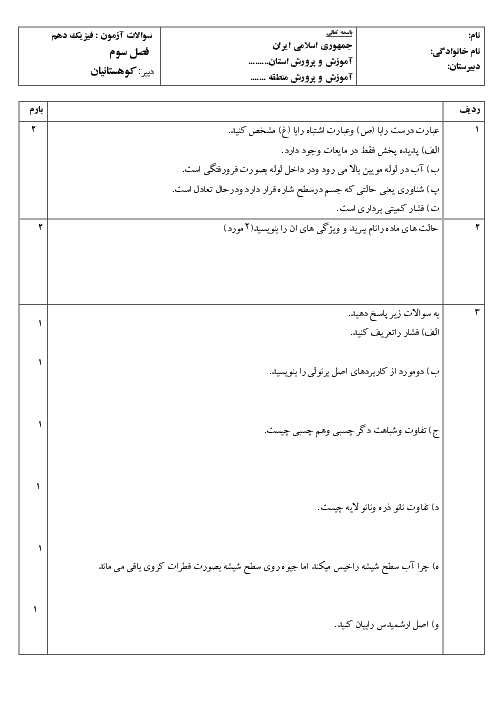
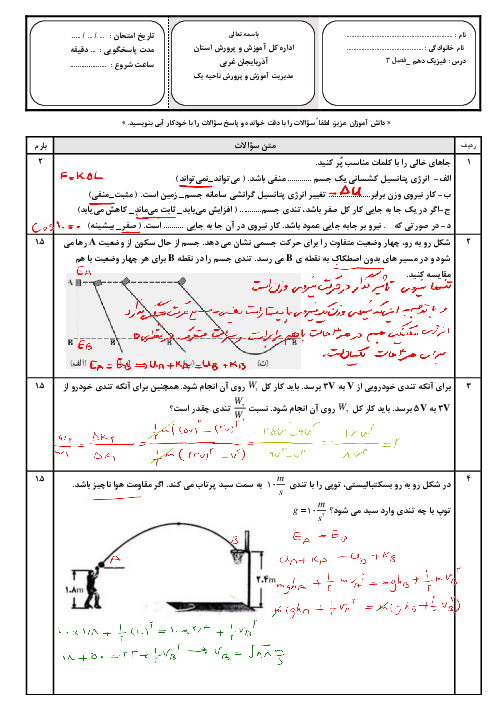
اگر حجم یک مول گاز در فشار 1atm و دمای $0{}^\circ C$ برابر 22/4Lit باشد، حجم 6g هیدروژن در فشار 2atm و دمای $182{}^\circ C$ چند لیتر است؟ (با فرض کامل بودن ${{M}_{{{H}_{2}}}}=2g/mol$)
پاسخ تشریحی :
ابتدا از روی جرم هیدروژن، تعداد مول آن را به دست میآوریم:
${{n}_{{{H}_{2}}}}=\frac{m{{H}_{2}}}{m{{H}_{2}}}=\frac{6}{2\times 1}=3mol$
$\left\{ \begin{matrix}{{P}_{{{H}_{2}}}}=2atm\begin{matrix}{} & {} & {} & {} \\\end{matrix} \\{{V}_{{{H}_{2}}=?}}\begin{matrix}{} & {} & {} \\\end{matrix}\begin{matrix}{} & {} & {} & {} \\\end{matrix} \\{{T}_{{{H}_{2}}}}=182+273=5\times 91 \\{{n}_{{{H}_{2}}}}=3mol\begin{matrix}{} & {} & {} & {} \\\end{matrix} \\\end{matrix} \right.$
$\left\{ \begin{matrix}{{P}_{0}}=1atm\begin{matrix}{} & {} & {} & {} \\\end{matrix} \\{{V}_{0}}=22/4Lit\begin{matrix}{} & {} & {} \\\end{matrix} \\{{T}_{0}}=273K=3\times 91K \\{{n}_{0}}=1mol\begin{matrix}{} & {} & {} & {} \\\end{matrix} \\\end{matrix} \right.$
با این دادهها میتوانیم به سراغ معادلهی حالت گازهای کامل برویم:
$\frac{{{P}_{{{O}_{2}}}}{{V}_{{{O}_{2}}}}}{{{T}_{{{O}_{2}}}}{{n}_{{{O}_{2}}}}}=\frac{{{P}_{0}}{{V}_{0}}}{{{T}_{0}}{{n}_{0}}}\Rightarrow \frac{2\times 5/6}{364\times {{n}_{{{O}_{2}}}}}=\frac{1\times 22/4}{273\times 1}\Rightarrow {{N}_{{{O}_{2}}}}=\frac{3}{8}mol$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!