درس 2: نمودارهای چند متغیره
ریاضی و آمار (1)
دهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
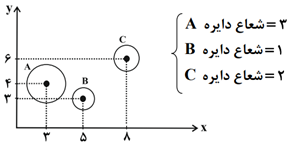
در نمودار حبابی مقابل، محور $x$ها، محور $y$ها و مساحت دايره‌ها به‌ترتيب طول، عرض و ارتفاع يک سری از جعبه‌ها به شكل مكعب مستطيل را نشان می‌دهند. حجم جعبهٔ ${A}'$ چند برابر حجم جعبهٔ ${B}'$ است؟ (راهنمايی: حجم مكعب مستطيل برابر است با طول ضرب در عرض ضرب در ارتفاع $\pi \simeq 3$)
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...