قسمت 2: حرکت هماهنگ ساده
فیزیک (3) تجربی
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
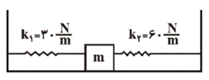
در شکل زیر، وزنه‌ی $m$ با دامنه‌ی ثابت روی یک سطح افقی بدون اصطکاک حرکت هماهنگ ساده انجام می‌دهد و بسامد زاویه‌ای‌اش برابر $\omega $ است. اگر فنر ${{k}_{2}}$ حذف شود، بسامد زاویه‌ای برابر ${\omega }'$ می‌شود. در این صورت نسبت $\frac{{{\omega }'}}{\omega }$ کدام است؟
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...