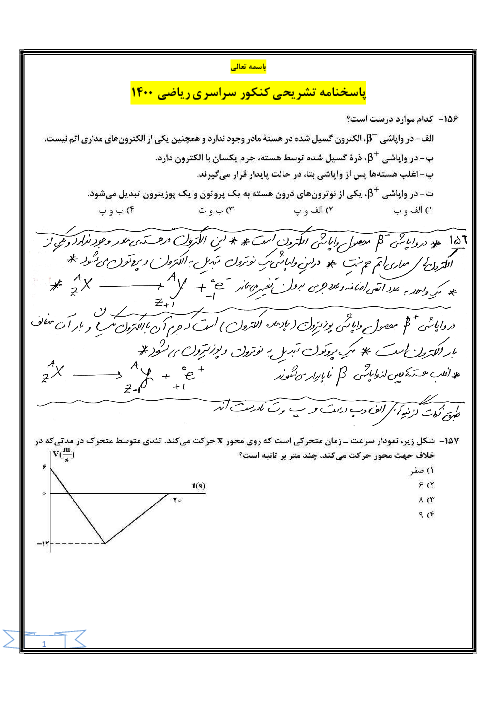
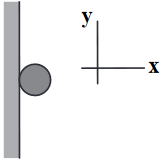
مطابق شکل مقابل، گلوله‌ٔ بارداری به جرم 20 گرم و بار $-۰/2$ میکروکولن در میدان الکتریکی یکنواخت $\overrightarrow{E}$ به دیوار قائم بدون اصطکاکی تکیه داده و در حال تعادل است. اگر نیروی عمودی دیوار به گلوله برابر 0/5 نیوتون باشد، میدان الکتریکی کدام است؟ $(g=10\frac{m}{{{s}^{2}}})$
$(2/5\times {{10}^{6}}\frac{N}{C}\overrightarrow{i})+(-{{10}^{6}}\frac{N}{C}\overrightarrow{j})$
2 )
$(2/5\times {{10}^{3}}\frac{N}{C}\overrightarrow{i})+({{10}^{3}}\frac{N}{C}\overrightarrow{j})$
3 )
$(-2/5\times {{10}^{3}}\frac{N}{C}\overrightarrow{i})+(-{{10}^{3}}\frac{N}{C}\overrightarrow{j})$
4 )
$(-2/5\times {{10}^{6}}\frac{N}{C}\overrightarrow{i})+({{10}^{6}}\frac{N}{C}\overrightarrow{j})$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...