درس 1: ماتریس و اعمال روی ماتریس‌ها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
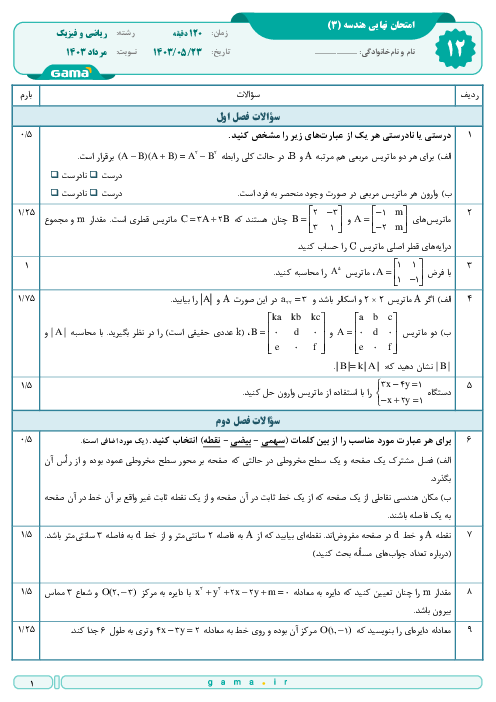
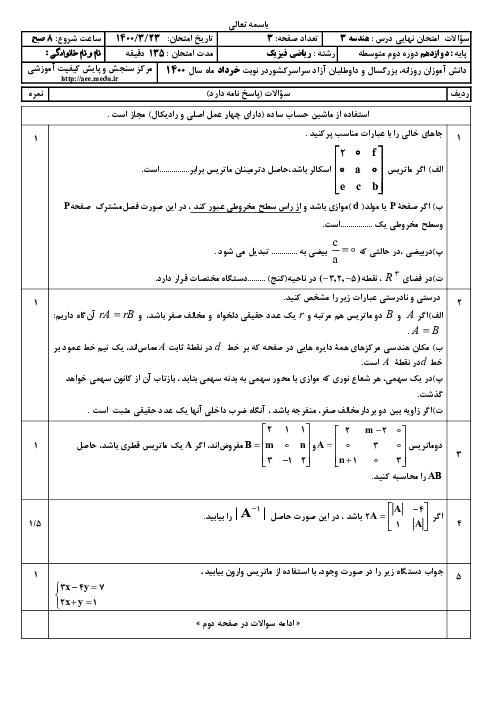
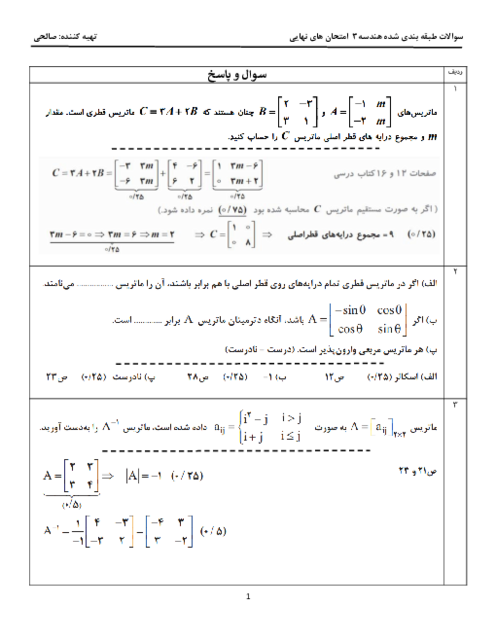
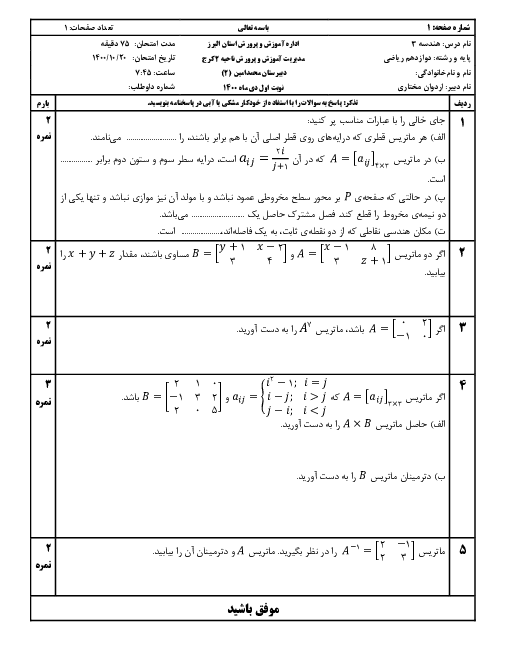
در دستگاه معادلات $\left\{ \begin{matrix} mx+3y={{b}_{1}} \\ 2mx+6y={{b}_{2}} \\\end{matrix} \right.$، به‌ازای کدام مقدار $\left[ \begin{matrix} {{b}_{1}} \\ {{b}_{2}} \\\end{matrix} \right]$، دستگاه بی‌شمار جواب دارد؟
1 )
$\left[ \begin{matrix} 2 \\ 1 \\\end{matrix} \right]$
2 )
$\left[ \begin{matrix} 3 \\ -4 \\\end{matrix} \right]$
$\left[ \begin{matrix} -1 \\ -2 \\\end{matrix} \right]$
4 )
$\left[ \begin{matrix} -3 \\ 4 \\\end{matrix} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...