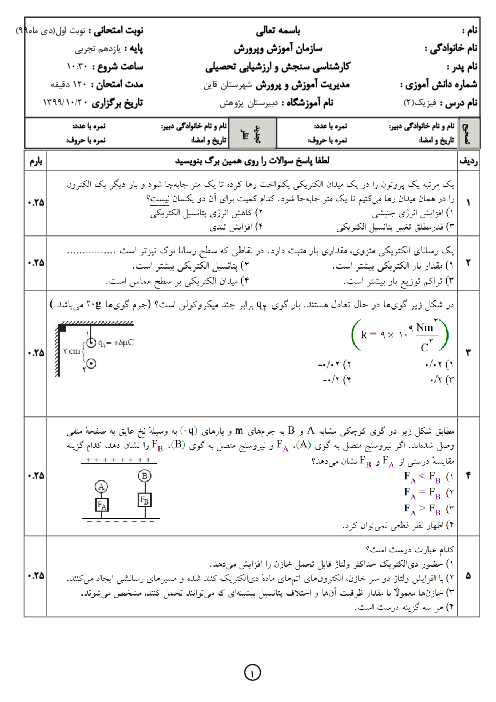
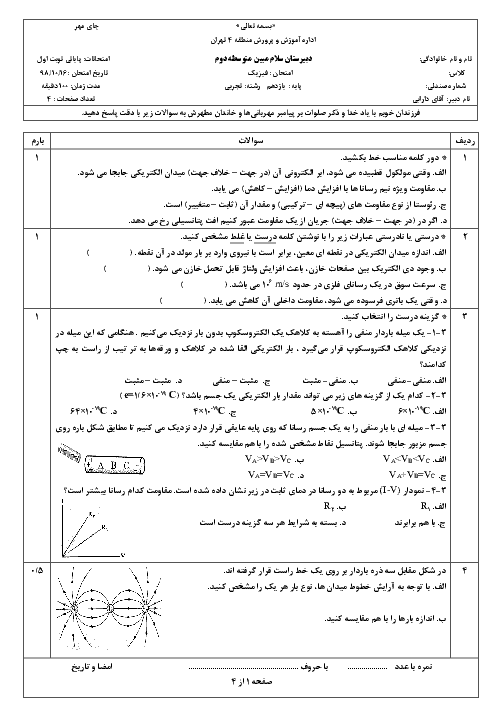
با توجه به رابطهٔ بزرگی میدان الکتریکی ناشی از یک بار الکتریکی داریم:
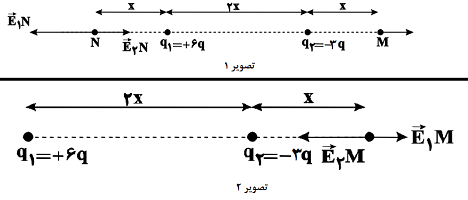
با توجه به تصویر 1
ابتدا اندازهٔ میدان برایند در نقطهٔ N را مییابیم:

$E=k\frac{\left| q \right|}{{{r}^{2}}}\Rightarrow \left\{ \begin{matrix}
   {{E}_{1N}}=\frac{k(6q)}{{{x}^{2}}}=\frac{6kq}{{{x}^{2}}}\Rightarrow {{\overrightarrow{E}}_{1N}}=-\frac{6kq}{{{x}^{2}}}\overrightarrow{i}  \\
   {{E}_{2N}}=\frac{k(3q)}{{{(3x)}^{2}}}=\frac{3kq}{9{{x}^{2}}}=\frac{kq}{3{{x}^{2}}}\Rightarrow {{\overrightarrow{E}}_{2N}}=\frac{kq}{3{{x}^{2}}}\overrightarrow{i}  \\
\end{matrix} \right.$

${{\overrightarrow{E}}_{N}}={{\overrightarrow{E}}_{1N}}+{{\overrightarrow{E}}_{2N}}\Rightarrow {{\overrightarrow{E}}_{N}}=-\frac{6kq}{{{x}^{2}}}\overrightarrow{i}+\frac{kq}{3{{x}^{2}}}\overrightarrow{i}\Rightarrow {{\overrightarrow{E}}_{N}}=-\frac{17}{3}\frac{kq}{{{x}^{2}}}\overrightarrow{i}\Rightarrow {{E}_{N}}=\frac{17}{3}\frac{kq}{{{x}^{2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

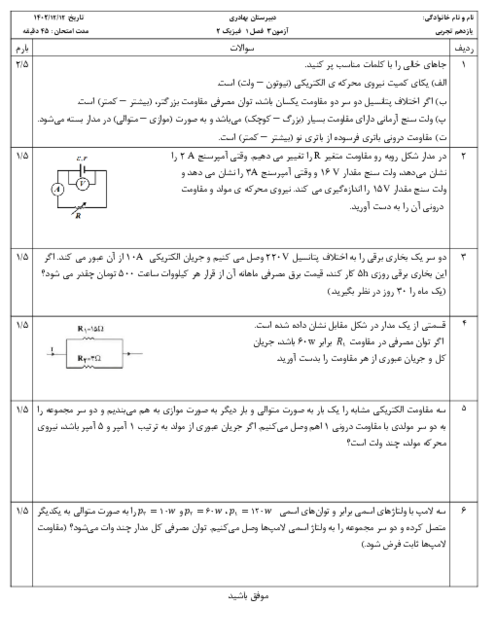
حال اندازهٔ میدان برایند در نقطهٔ M را می‌یابیم:
با توجه به تصویر 2

${{E}_{1M}}=\frac{k(6q)}{{{(3x)}^{2}}}=\frac{6kq}{9{{x}^{2}}}=\frac{2}{3}\frac{kq}{{{x}^{2}}}\Rightarrow {{\overrightarrow{E}}_{1M}}=\frac{2}{3}\frac{kq}{{{x}^{2}}}\overrightarrow{i}$
${{E}_{2M}}=\frac{k(3q)}{{{x}^{2}}}=\frac{3kq}{{{x}^{2}}}\Rightarrow {{\overrightarrow{E}}_{2M}}=-\frac{3kq}{{{x}^{2}}}\overrightarrow{i}\,\Rightarrow {{\overrightarrow{E}}_{M}}={{\overrightarrow{E}}_{1M}}+{{\overrightarrow{E}}_{2M}}\Rightarrow {{\overrightarrow{E}}_{M}}=\frac{2}{3}\frac{kq}{{{x}^{2}}}\overrightarrow{i}-3\frac{kq}{{{x}^{2}}}\overrightarrow{i}=-\frac{7}{3}\frac{kq}{{{x}^{2}}}\overrightarrow{i}\Rightarrow {{E}_{M}}=\frac{7}{3}\frac{kq}{{{x}^{2}}}\,\,\,\,\,\,\,\,\,(2)$
$\xrightarrow[{}]{(2),(1)}\,\frac{{{E}_{M}}}{{{E}_{N}}}=\frac{\frac{7}{3}\frac{kq}{{{x}^{2}}}}{\frac{17}{3}\frac{kq}{{{x}^{2}}}}\Rightarrow \frac{{{E}_{M}}}{E}=\frac{7}{17}\Rightarrow {{E}_{M}}=\frac{7}{17}E$