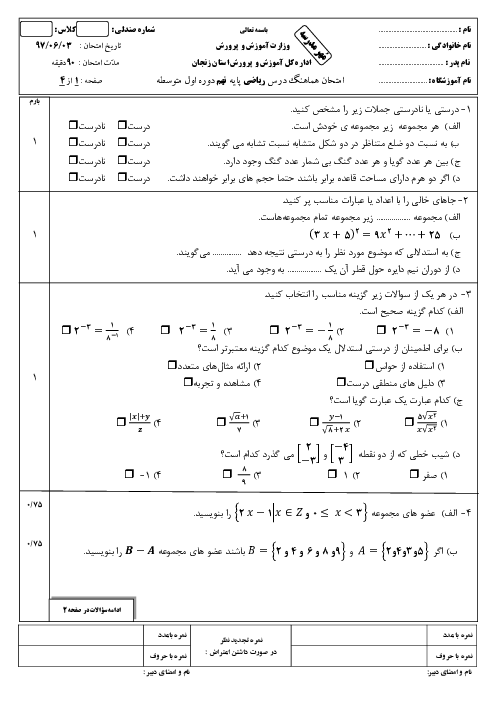
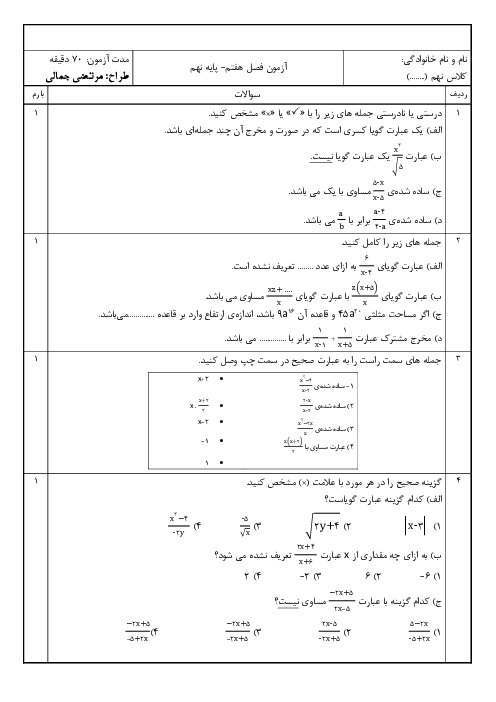
در شکل زیر کمانی به مرکز A و به شعاع AB زده‌ایم تا محور اعداد را در نقطه C قطع کند، اگر $AM = MO = OB = 1$، در این صورت C چه عددی را نشان می‌دهد؟ (O مبدأ است $\hat M = B\hat OA = {90^ \circ }$)
1 )
$\sqrt 2 - \sqrt 3 $
$\sqrt {{{(\sqrt 3 - \sqrt 2 )}^2}} $
3 )
$\left| { - \sqrt 2 - \sqrt 3 } \right|$
4 )
$1 + \sqrt 3 $
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...