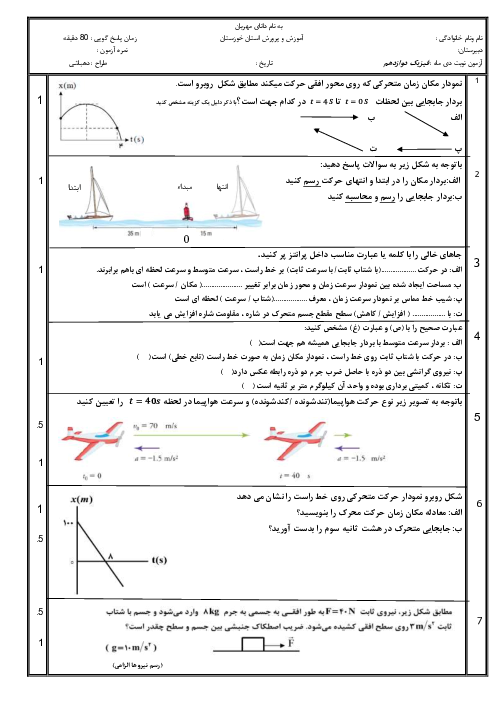
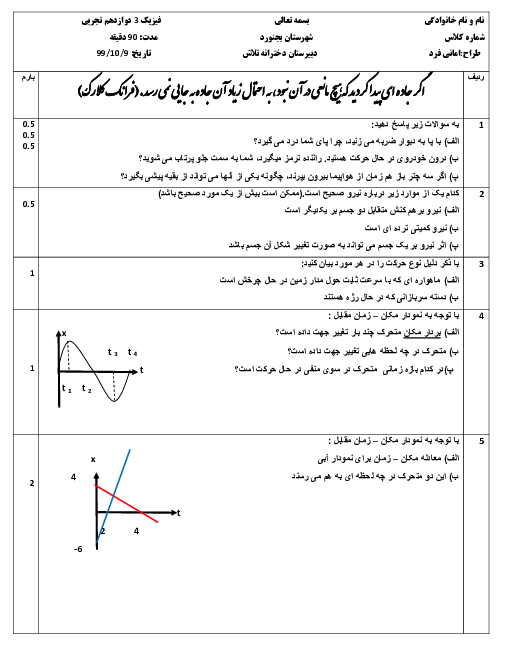
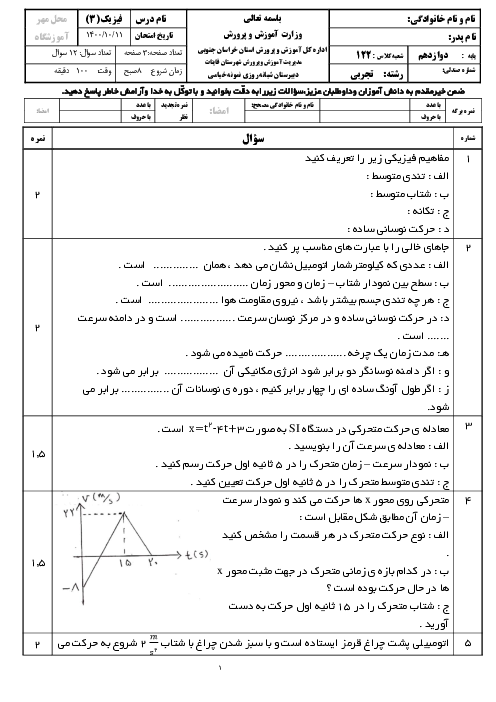
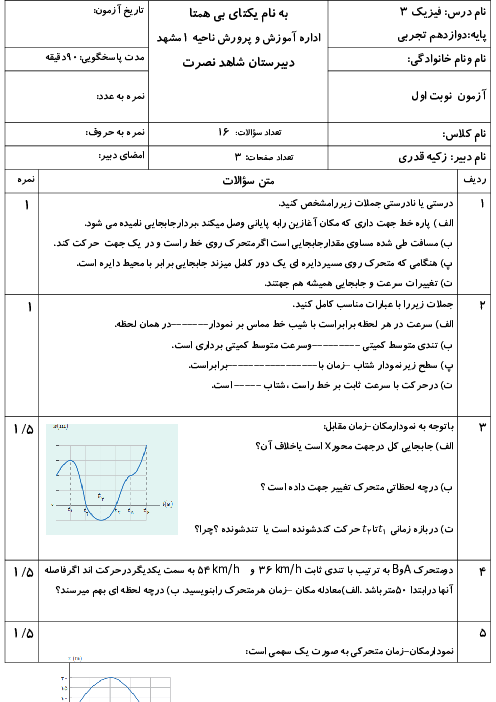
جسمی به جرم $2kg$ با تندی $v$ به یک فنر افقی با طول اولیهٔ $12cm$ و ثابت $200\frac{N}{m}$ برخورد می‌کند. اگر ضریب اصطکاک جنبشی جسم با سطح افقی برابر با $0/2$ باشد، در لحظه‌ای که اندازهٔ شتاب جسم بیشینه و برابر با $5\frac{m}{{{s}^{2}}}$ می‌شود، طول فنر چند سانتی متر است؟ $(g=10\frac{N}{kg})$
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...