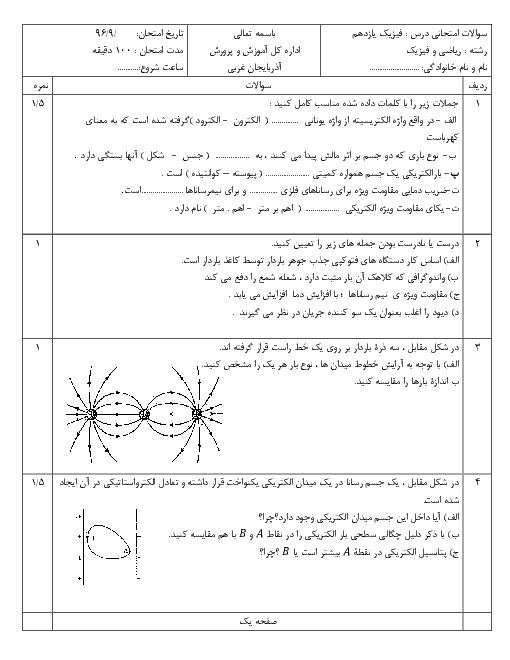
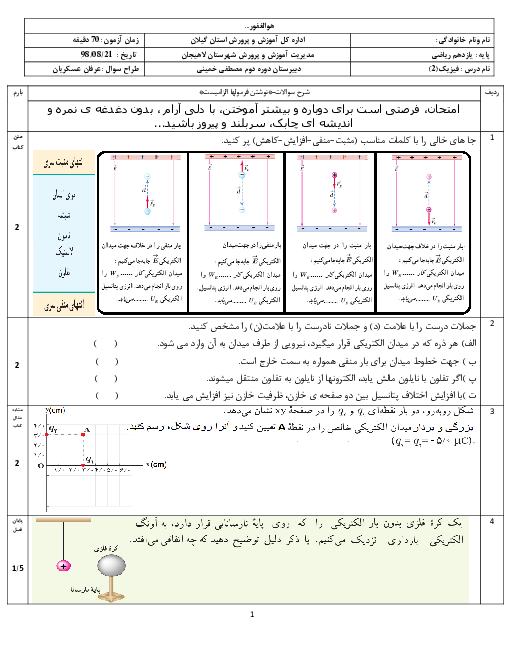
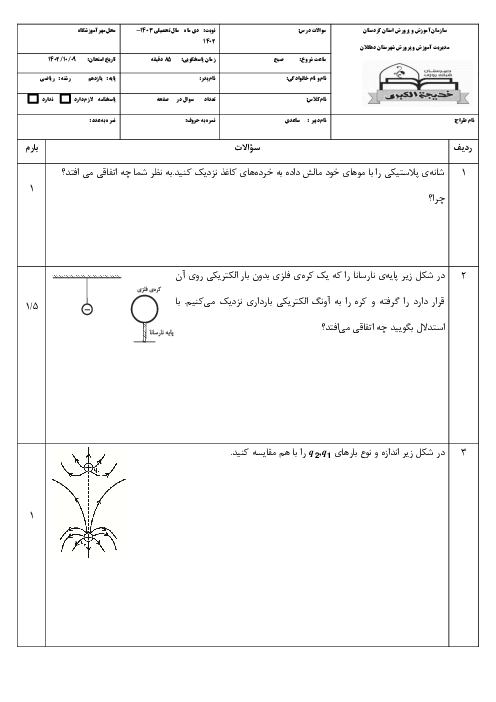
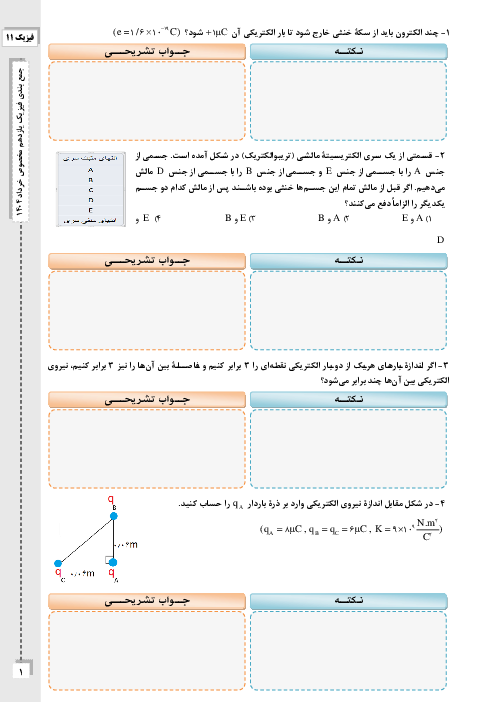
$R=\rho \frac{L}{A}\Rightarrow \frac{{{R}_{2}}}{{{R}_{1}}}=\frac{{{\rho }_{2}}}{{{\rho }_{1}}}\times \frac{{{L}_{2}}}{{{L}_{1}}}\times \frac{{{A}_{1}}}{{{A}_{2}}}$         (1)

از آن‌جا كه دما تنها روی $\rho $ تأثير می‌گذارد ابتدا نسبت $\frac{{{\rho }_{2}}}{{{\rho }_{1}}}$ را می‌یابيم: 

${{\rho }_{2}}={{\rho }_{1}}(1+\alpha (T-{{T}_{{}^\circ }}))$

$\Rightarrow \frac{{{\rho }_{2}}}{{{\rho }_{1}}}=1+4\times {{10}^{-4}}\times (400-200)=1/08$           (2)

حال تأثير كاهش شعاع را می‌یابيم:

${{m}_{1}}={{m}_{2}}\Rightarrow {{{\rho }'}_{1}}{{V}_{1}}={{{\rho }'}_{2}}{{V}_{2}}$

$\xrightarrow{:{{{{\rho }'}}_{1}}={{{{\rho }'}}_{2}}}{{V}_{1}}={{V}_{2}}\xrightarrow{V=AL}{{A}_{1}}{{L}_{1}}={{A}_{2}}{{L}_{2}}$

$\frac{{{L}_{2}}}{{{L}_{1}}}=\frac{{{A}_{1}}}{{{A}_{2}}}\xrightarrow{A=\pi {{r}^{2}}}\frac{{{L}_{2}}}{{{L}_{1}}}={{(\frac{{{r}_{1}}}{{{r}_{2}}})}^{2}}={{(\frac{R}{\frac{R}{2}})}^{2}}=4$         (3)

بنابراين با توجه به رابطه‌های (1) ،(2) و (3) داريم: 

$\frac{{{R}_{2}}}{{{R}_{1}}}=1/08\times 4\times 4=17/28$