پودمان 3: زاویه‌های دلخواه و نسبت‌های مثلثاتی آنها
ریاضی2 فنی
یازدهم
دوره دوم متوسطه- فنی
مشترک شاخۀ فنی و حرفه‌ای
درسنامه آموزشی این مبحث
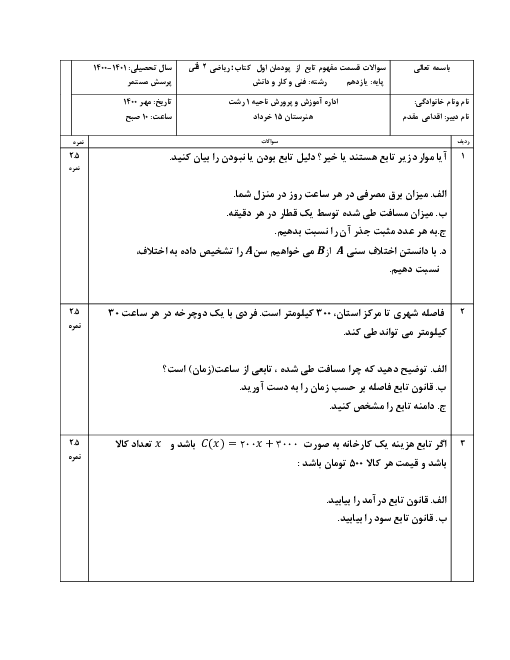
اگر $\cos \theta = \frac{2}{7}$ و $\theta $ در ناحیه‌ی چهارم مثلثاتی باشد، مقدار $\tan \theta $ کدام است؟
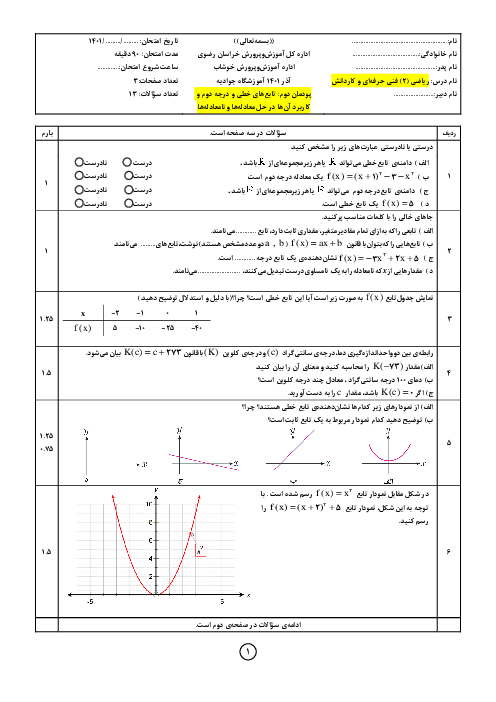
1 )
$ - \frac{{3\sqrt 5 }}{2}$
2 )
$\frac{{3\sqrt 5 }}{2}$
3 )
$\frac{{2\sqrt 5 }}{{15}}$
$ - \frac{{2\sqrt 5 }}{{15}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...