قسمت 3: حرکت با شتاب ثابت
فیزیک (3) تجربی
دوازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
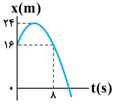
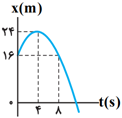
نمودار مكان - زمان متحركی مطابق شكل زير و بهصورت سهمی است. در بازهٔ زمانی $t=0$ تا $t=8s$ اندازهٔ شتاب متوسط و سرعت متوسط متحرک در $SI$، كدام است؟