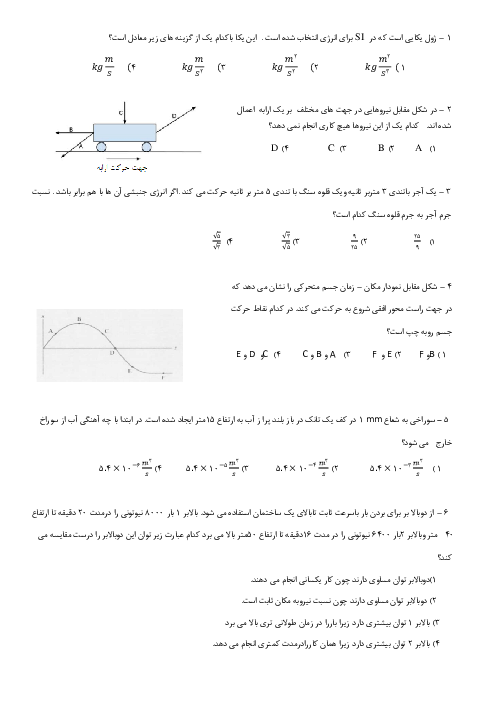
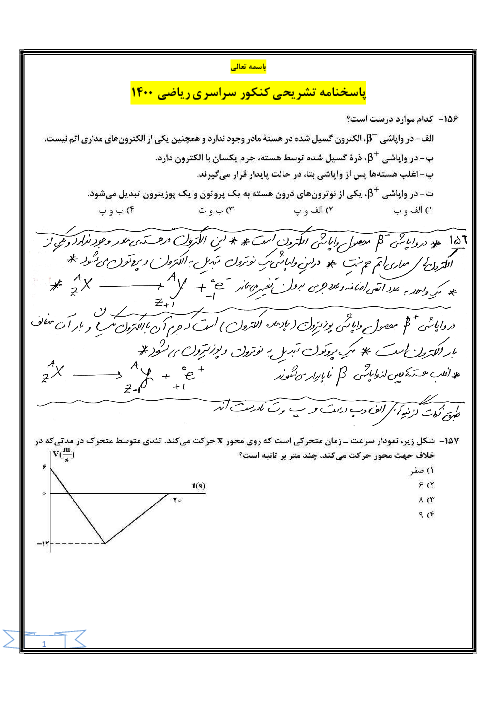
گام اول: با توجه به اطلاعات تست و مطابق شکل زیر مدت‌زمان حرکت متحرک (1) از $A$ به $B$ با مدت‌زمان حرکت متحرک (2) از $C$ به $B$ برابر است، بنابراین:

${t_1} = {t_2} \Rightarrow \frac{{{x_1}}}{{{v_1}}} = \frac{{{x_2}}}{{{v_2}}} \Rightarrow \frac{{{v_2}}}{{{v_1}}} = \frac{x}{{180 - x}}\,\,\,(I)$

گام دوم: از طرفی متحرک (1) مسافت $x$ را در مدت $16s$ و متحرک (2) مسافت $180 - x$ را در مدت $25s$ طی می‌کند، پس می‌توان نوشت:

$\left\{ {\begin{array}{*{20}{c}}{x = {v_1} \times 16}\\{180 - x = {v_2} \times 25}\end{array} \Rightarrow \frac{x}{{180 - x}} = \frac{{{v_1}}}{{{v_2}}}} \right. \times \frac{{16}}{{25}}\,\,\,(II)$

با توجه به روابط $(I)$ و $(II)$ می‌توان نوشت:

$(I),(II) \Rightarrow \frac{{{v_2}}}{{{v_1}}} = \frac{{{v_1}}}{{{v_2}}} \times \frac{{16}}{{25}} \Rightarrow {(\frac{{{v_2}}}{{{v_1}}})^2} = \frac{{16}}{{25}} \Rightarrow \frac{{{v_2}}}{{{v_1}}} = \frac{4}{5}$

گام سوم: نسبت به دست آمده برای سرعت‌ها را در رابطهٔ $(I)$ قرار می‌دهیم تا $x$ به دست بیاید.

$\frac{x}{{180 - x}} = \frac{4}{5} \Rightarrow 5x = 4 \times 180 - 4x \Rightarrow 9x = 4 \times 180$

$ \Rightarrow x = 4 \times 20 = 80m$

حالا با توجه به این‌که $x = 16{v_1}$، سرعت متحرک (1) را به دست می‌آوریم:

$80 = 16 \times {v_1} \Rightarrow {v_1} = 5m/s$