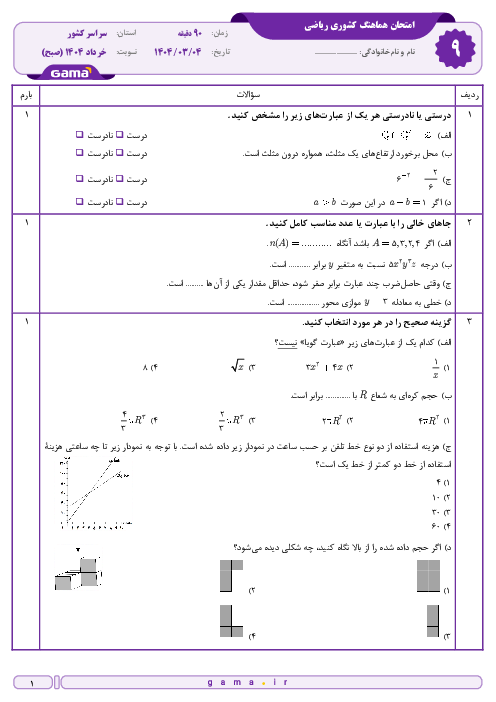
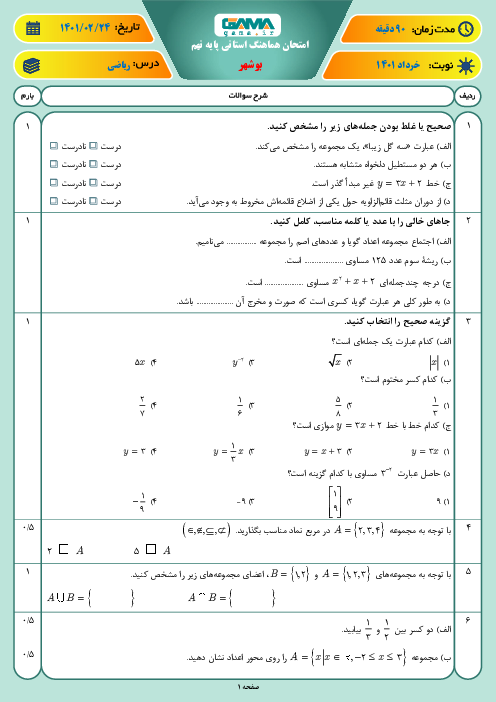
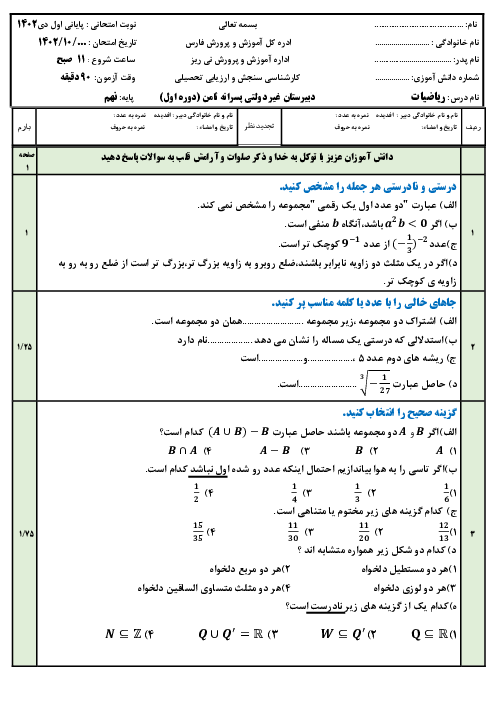
می‌دانیم $\sqrt[n]{{a \times b}} = \sqrt[n]{a} \times \sqrt[n]{b}$

تک تک عبارات رادیکالی را باز می‌کنیم.

$\sqrt {12}  = \sqrt {4 \times 3}  = \sqrt 4  \times \sqrt 3  = 2 \times \sqrt 3  = 2\sqrt 3 $

$\sqrt {147}  = \sqrt {49 \times 3}  = \sqrt {49}  \times \sqrt 3  = 7 \times \sqrt 3  = 7\sqrt 3 $

$\sqrt {48}  = \sqrt {16 \times 3}  = \sqrt {16}  \times \sqrt 3  = 4 \times \sqrt 3  = 4\sqrt 3 $

$\frac{{3\sqrt {12}  - \sqrt {147}  + \sqrt {48} }}{{3\sqrt 6 }} = \frac{{6\sqrt 3  - 7\sqrt 3  + 4\sqrt 3 }}{{3\sqrt 6 }} = \frac{{\mathop {\cancel{3}}\limits^1 \sqrt 3 }}{{\cancel{3}\sqrt 6 }} = \frac{{ - \mathop {\cancel{{\sqrt 3 }}}\limits^1 }}{{\sqrt 2  \times \cancel{{\sqrt 3 }}}} = \frac{{ - 1}}{{\sqrt 2 }} \times \frac{{\sqrt 2 }}{{\sqrt 2 }} =  - \frac{{\sqrt 2 }}{2}$