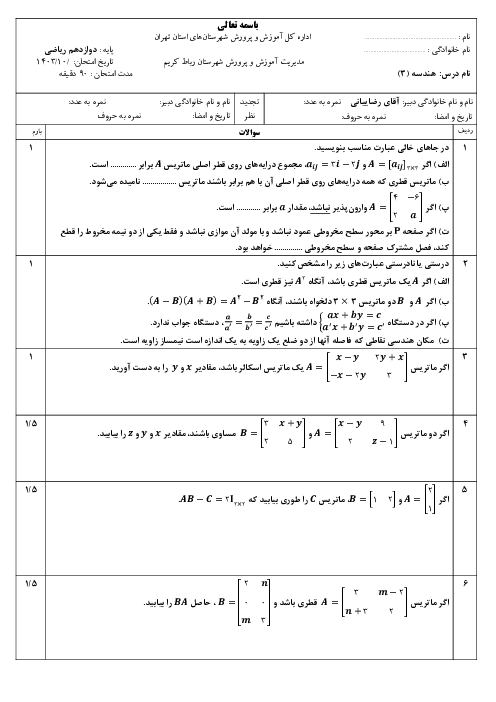
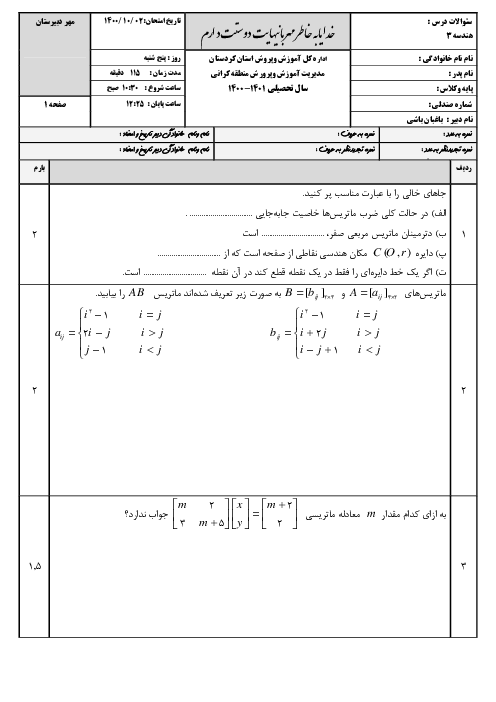
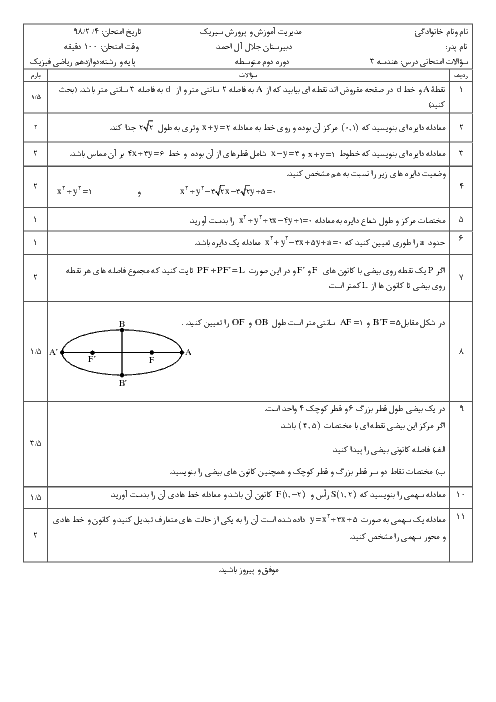
ابتدا ماتریس $C$ را معلوم می‌کنیم:

 $C=\left[ \begin{matrix}
   1 & 3 & 6 & 24  \\
   \frac{1}{3} & 1 & 2 & 8  \\
   \frac{1}{6} & \frac{1}{2} & 1 & 4  \\
   \frac{1}{24} & \frac{1}{8} & \frac{1}{4} & 1  \\
\end{matrix} \right]$

همان‌طور که می‌بینید سطرهای دوم، سوم و چهارم، مضرب سطر اول هستند (اگر سطر اول را در $\frac{1}{3}$ ضرب کنیم، سطر دوم و اگر آن را در $\frac{1}{6}$ ضرب کنیم، سطر سوم و اگر آن را در $\frac{1}{24}$ ضرب کنیم، سطر چهارم به دست می‌آید). پس داریم:

 ${{C}^{2}}=tr(C)\times C\Rightarrow {{C}^{2}}=(1+1+1+1)C\Rightarrow {{C}^{2}}=4C\Rightarrow {{C}^{2}}=\left[ \begin{matrix}
   4 & \bigcirc  & \bigcirc  & \bigcirc   \\
   \bigcirc  & 4 & \bigcirc  & \bigcirc   \\
   \bigcirc  & \bigcirc  & 4 & \bigcirc   \\
   \bigcirc  & \bigcirc  & \bigcirc  & 4  \\
\end{matrix} \right]$

بنابراین مجموع درایه‌های قطر اصلی ${{C}^{2}}$ برابر $16$ است.