نكته (قضيه‌ی كسينوس‌ها): در مثلث دلخواه ABC داریم:

$\left\{ \begin{matrix}
   {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\operatorname{Cos}\hat{A}  \\
   {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\operatorname{Cos}\hat{B}  \\
   {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\operatorname{Cos}\hat{C}  \\
\end{matrix} \right.$

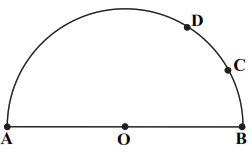
مطابق شکل، زاویه‌ی $A\hat{C}B$ زاویه‌ی محاطی روبه‌رو به قطر است، پس قائم است. به‌کمک قضیه‌ی فیثاغوس در مثلث ABC، داریم:

$A{{C}^{2}}+B{{C}^{2}}=A{{B}^{2}}\Rightarrow A{{C}^{2}}+4=64\Rightarrow A{{C}^{2}}=60\Rightarrow AC=2\sqrt{15}$

از طرفی چهارضلعی ABCD محاطی است، پس زوایای مقابل آن مکمل‌اند: 

$\hat{B}+\hat{D}={{180}^{{}^\circ }}\Rightarrow \hat{D}={{180}^{{}^\circ }}-\hat{B}\,\,\,\,\,(*)$

و در مثلث ACBبه‌کمک نسبت کسینوس، داریم:

$\operatorname{Cos}\hat{B}=\frac{BC}{AB}=\frac{2}{8}=\frac{1}{4}\xrightarrow{(*)}\operatorname{Cos}\hat{D}=\operatorname{Cos}({{180}^{{}^\circ }}-\hat{B})=-\operatorname{Cos}\hat{B}=-\frac{1}{4}$

و یانک با توجه به نکته در مثلث ADC، خواهیم داشت:

$\begin{align}
  & A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}-2(AD)(DC)\operatorname{Cos}\hat{D}\Rightarrow 60=A{{D}^{2}}+4-2(AD)(2)(-\frac{1}{4}) \\ 
 & \Rightarrow A{{D}^{2}}+AD-56=0\Rightarrow (AD+8)(AD-7)=0\Rightarrow \left\{ \begin{matrix}
   AD=-8  \\
   AD=7  \\
\end{matrix} \right. \\ 
\end{align}$