از هر یک از کلاس‌های A و B ده دانش‌آموز را به طور تصادفی انتخاب می‌کنیم. اگر معدل آن‌ها به صورت زیر باشد، کدام کلاس عملکرد بهتری داشته است؟

موبایل / ایمیل

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل / ایمیل

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

ورود | ثبت نام

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 3: معیارهای پراکندگی ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

از هر یک از کلاس‌های A و B ده دانش‌آموز را به طور تصادفی انتخاب می‌کنیم. اگر معدل آن‌ها به صورت زیر باشد، کدام کلاس عملکرد بهتری داشته است؟

$\begin{align}
& A:16,15,14,14,16,15,15,14,18,13 \\
& B:15,18,13,15,14,16,15,15,16,13 \\
\end{align}$

1 )

2 )

3 )

هر دو یکسان

4 )

نمی‌توان تعیین کرد.

نمایش پاسخ

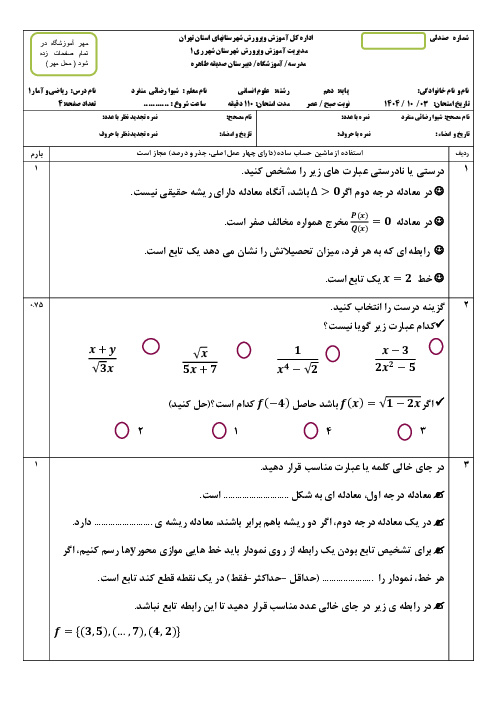
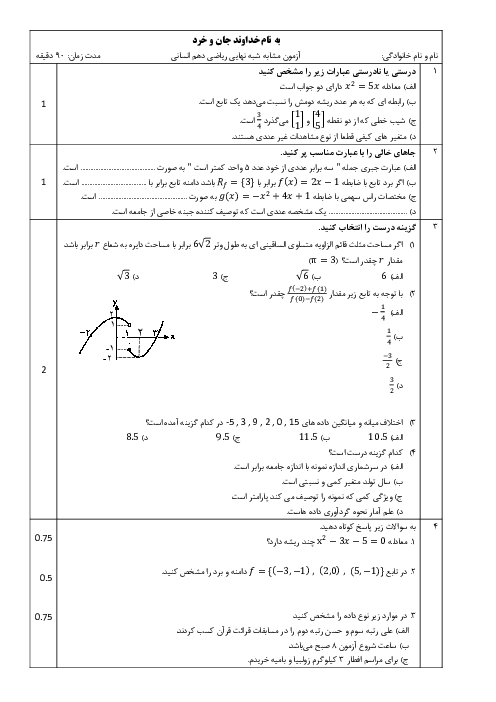
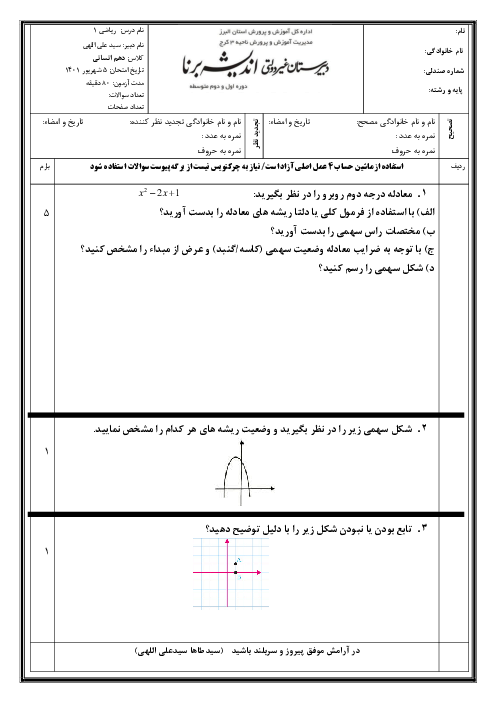
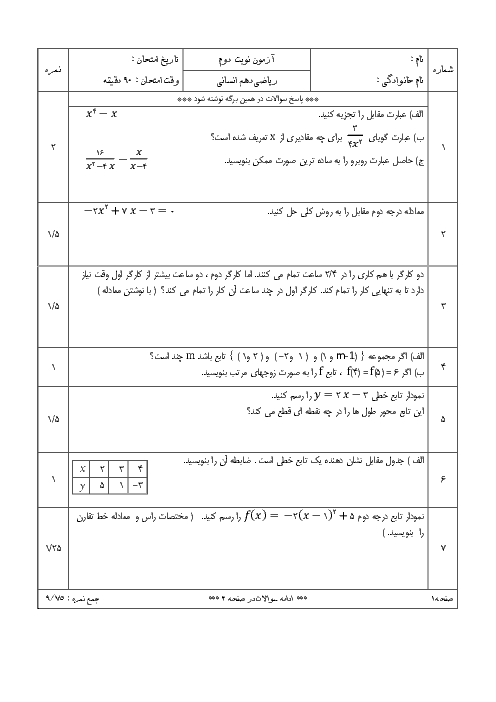
$\begin{align}
& A:13,14,14,14,15,15,15,16,16,18 \\
& B:13,13,14,15,15,15,15,16,16,18 \\
& {{R}_{A}}={{R}_{B}}=18-13=5 \\
& {{{\bar{x}}}_{A}}=\frac{13+14+14+14+15+15+15+16+16+18}{10}=\frac{150}{10}=15 \\
& {{{\bar{x}}}_{B}}=\frac{13+13+14+15+15+15+15+16+16+18}{10}=\frac{150}{10}=15 \\
& \sigma _{A}^{2}=\frac{{{(13-15)}^{2}}+3{{(14-15)}^{2}}+3{{(15-15)}^{2}}+2{{(16-15)}^{2}}+{{(18-15)}^{2}}}{10}=\frac{18}{10}=1/8 \\
& \sigma _{B}^{2}=\frac{2{{(13-15)}^{2}}+{{(14-15)}^{2}}+4{{(15-15)}^{2}}+2{{(16-15)}^{2}}+{{(18-15)}^{2}}}{10}=\frac{20}{10}=2 \\
\end{align}$

$\sigma _{B}^{2} \gt \sigma _{A}^{2}$ پس $A$ عملکرد بهتری داشته است.

گزارش اشکال