درس 1: تبدیل نمودار توابع
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
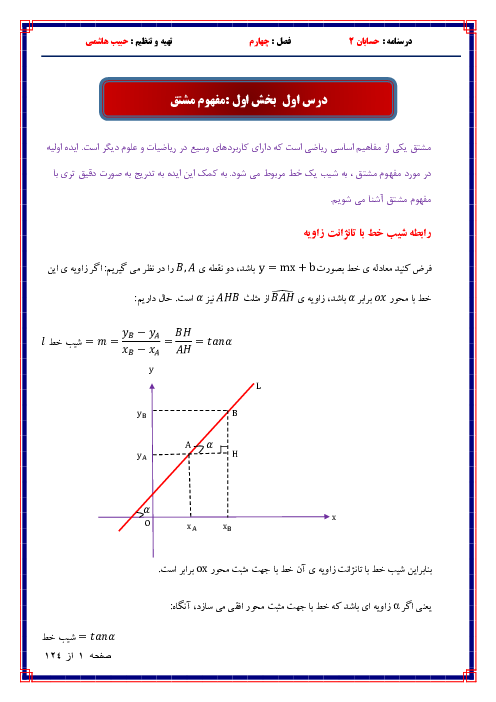
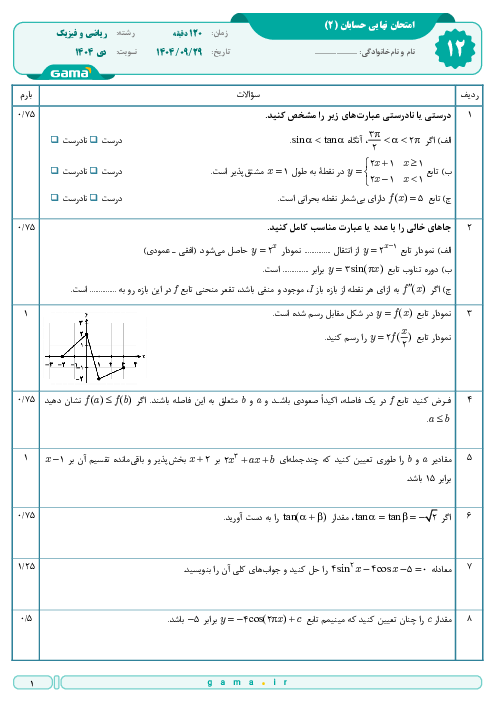
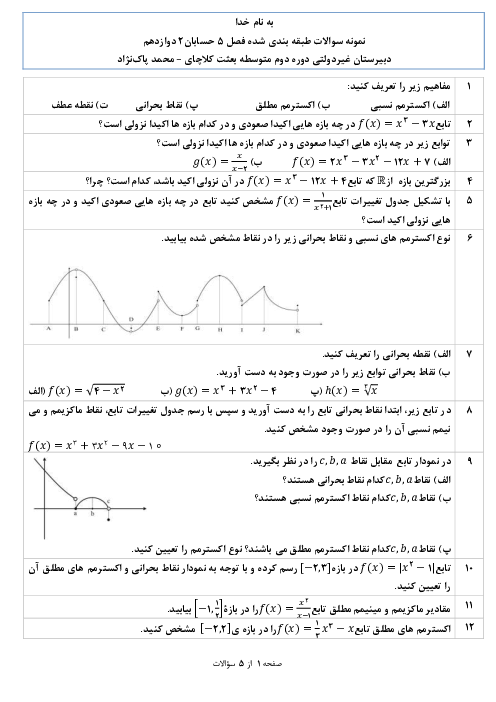
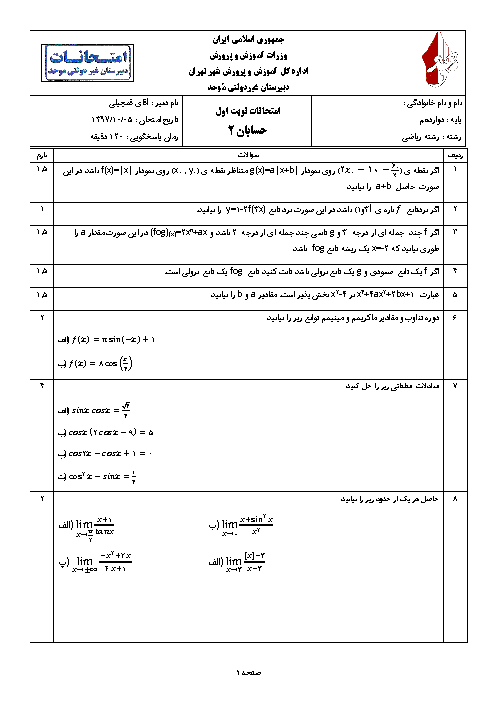
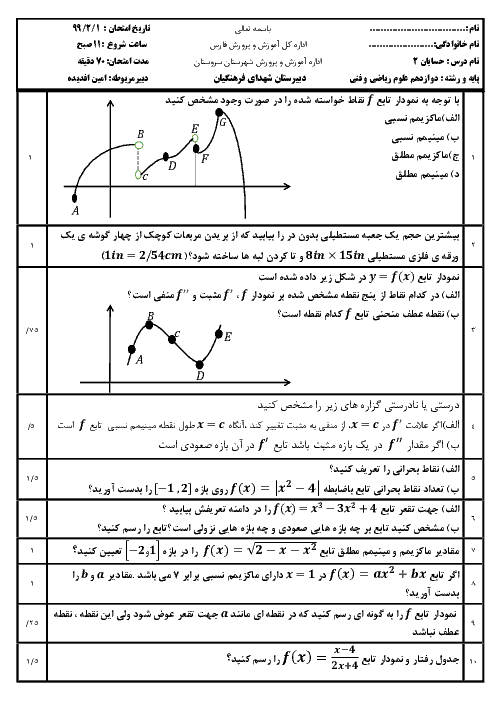
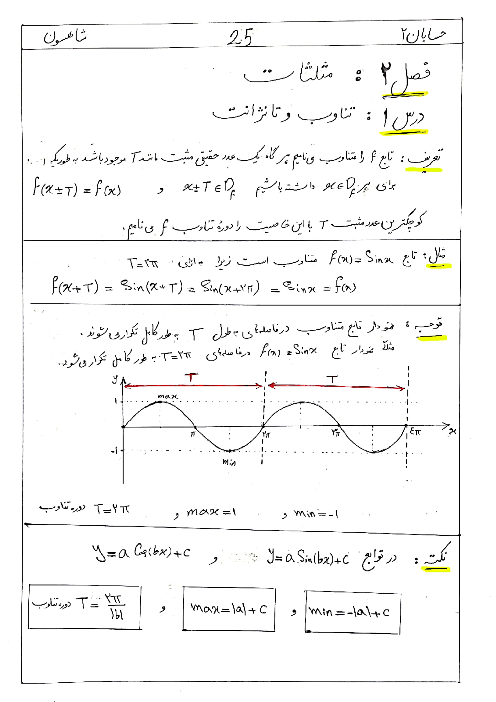
اگر نقطه‌ی $(\frac{1-{{x}_{0}}}{2},{{y}_{0}}+1)$ روی نمودار $g$ متناظر نقطه‌ی $({{x}_{0}},{{y}_{0}})$ روی نمودار $f$ باشد. رابطه‌ی بین $f$ و $g$ به کدام صورت است؟
1 )
$f(x)=g(1-2x)-1$
$g(x)=f(1-2x)+1$
3 )
$f(x)=g(\frac{1-x}{2})+1$
4 )
$g(x)=f(\frac{1-x}{2})-1$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...