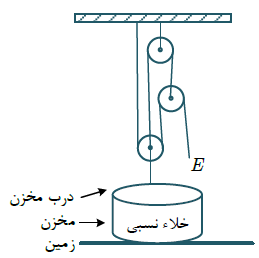
قدم اول: نیروی لازم برای برداشتن درب ظرف را از رابطه فشار فصل 8 محاسبه می‌کنیم. مساحت سطح * فشار = نیرو * توجه: به یکاهای داده شده دقت کنید. فشار $ \div 10000 = 10N/c{m^2} \to $ تبدیل نیوتون بر مترمربع $ = 1 \times {10^5}pa$ $F = P \times A = 10N/c{m^2} \times 4cm \times 4cm \times 3 = 480N$ چون قطر 8 است پس شعاع 4 خواهد بود و مساحت دایره از رابطه زیر به دست می‌آید. 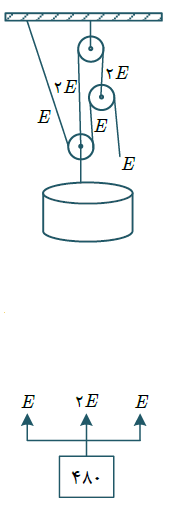شعاع $ \times $ شعاع = مساحت دایره $ \times \,\pi $ این 480 نیوتن نیروی مقاوم است که باید بر آن غلبه کنیم، پس: $R = 480N$ حال سراغ قرقره‌ها رفته و مزیت را محاسبه می‌کنیم: اگر نخ را با نیروی E بکشیم، ادامة آن نیز با نیروی E کشیده می‌شود، نخ متصل به قرقره وسط که ثابت است با نیروی  کشیده می‌شود، همانطور که می‌بینید وزنه با نیروهای نشان داده شده کشیده می‌شود. پس مزیت دستگاه 4 می‌شود. ($A = 4$) نیروی مقاوم تقسیم بر نیروی محرک = مزیت مکانیکی نیروی مقاوم تقسیم بر مزیت مکانیکی = نیروی محرک $ = E = \frac{R}{A} = \frac{{480N}}{4} = 120N$