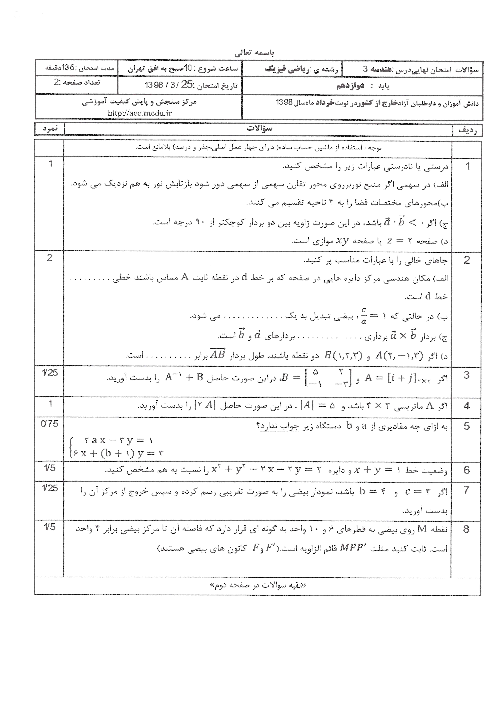
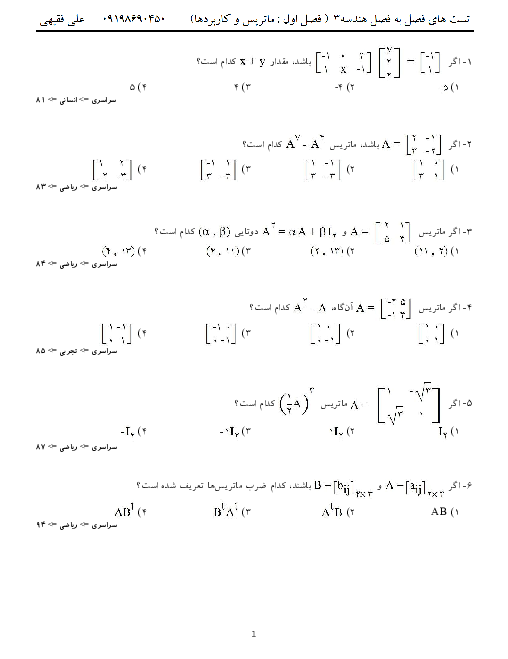
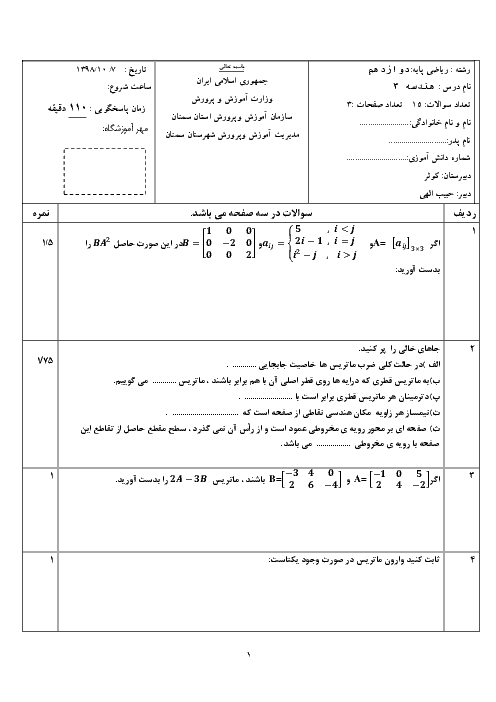
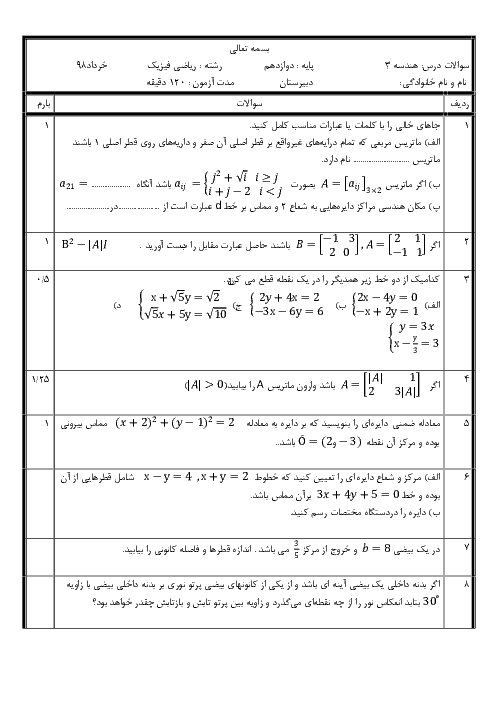
ابتدا ماتریسهای $A$ و $B$ را به دست میآوریم:
$A=\left[ \begin{matrix}
0 & -3 \\
1 & -2 \\
\end{matrix} \right],B=\left[ \begin{matrix}
3 \\
5 \\
\end{matrix}\,\,\begin{matrix}
4 \\
6 \\
\end{matrix}\,\,\begin{matrix}
5 \\
7 \\
\end{matrix} \right]$
حال ماتریس $AB$ را محاسبه میکنیم:
$AB=\left[ \begin{matrix}
0 & -3 \\
1 & -2 \\
\end{matrix} \right]\left[ \begin{matrix}
3 \\
5 \\
\end{matrix}\,\,\,\begin{matrix}
4 \\
6 \\
\end{matrix}\,\,\,\begin{matrix}
5 \\
7 \\
\end{matrix} \right]=\left[ \begin{matrix}
-15 \\
-7 \\
\end{matrix}\,\,\,\,\begin{matrix}
-18 \\
-8 \\
\end{matrix}\,\,\,\,\begin{matrix}
-21 \\
-9 \\
\end{matrix} \right]\Rightarrow $ کوچکترین درایه، درایۀ سطر اول و ستون سوم است