اگر نقطهٔ عطف نمودار تابع با ضابطهٔ باشد، آنگاه مقدار کدام است؟ | حسابان (2) دوازدهم شماره 85068 - گاما

Loading [MathJax]/jax/output/CommonHTML/jax.js

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

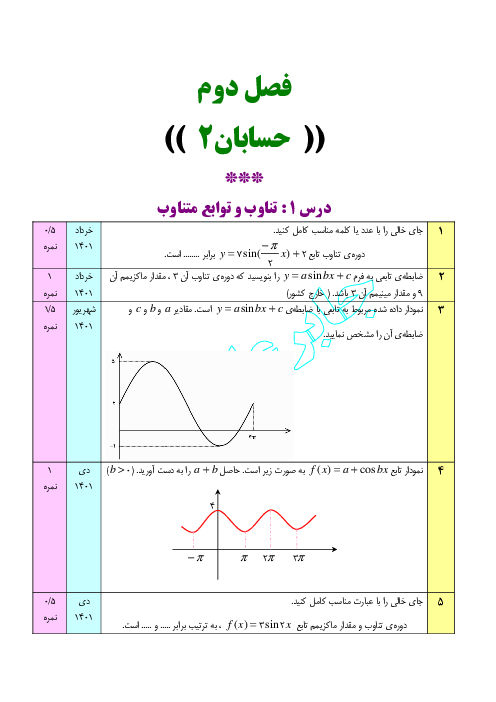
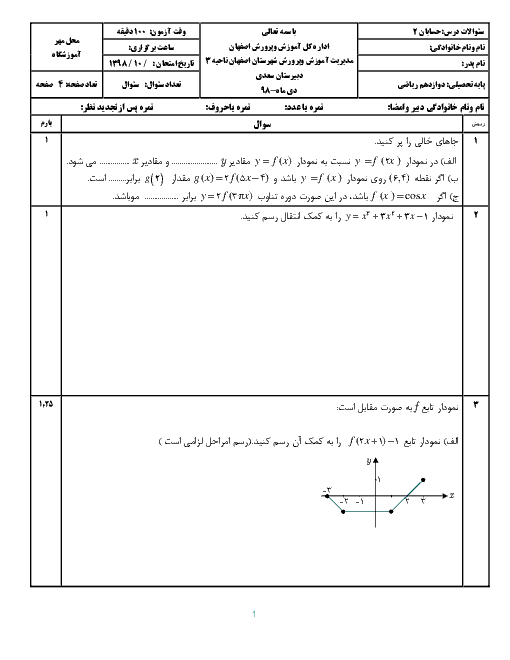
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

اگر $A(1,-11)$ نقطهٔ عطف نمودار تابع با ضابطهٔ $f(x)={{x}^{3}}+a{{x}^{2}}+bx$ باشد، آنگاه مقدار $f(-1)$ کدام است؟

1 )

3

2 )

4

3 )

5

4 )

6

نمایش پاسخ

از اینکه $A(1,-11)$ نقطهٔ عطف نمودار تابع $f$ است، می‌توان نتیجه گرفت:

۱) مشخصات نقطهٔ $A(1,-11)$ در معادلهٔ تابع صدق می‌کند:

$\begin{align} & A(1,-11)\in f \\ & \Rightarrow f(1)=-11\Rightarrow 1+a+b=-11\Rightarrow a+b=-12\,\,\,\,(*) \\ \end{align}$

2) مشتق دوم تابع $f$ در $x=1$ برابر صفر است.

$f(x)={{x}^{3}}+a{{x}^{2}}+bx$

$\Rightarrow f'(x)=3{{x}^{2}}+2ax+b$

$\Rightarrow f''(x)=6x+2a\Rightarrow f''(1)=0\Rightarrow 6+2a=0$

$\Rightarrow a=-3\xrightarrow{(*)}b=-9$

$\Rightarrow f(x)={{x}^{3}}-3{{x}^{2}}-9x\Rightarrow f(-1)=-1-3+9=5$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1403/03/18

عباس ابراهیمی علویجه

ویدیو دوره آموزشی، حسابان (2) دوازدهم دوره دوم متوسطه- نظری

مدرس: سید حجت طبائی

مدت دوره: 3 ساعت (5 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

جامعه شناسی (3)

جامعه شناسی (3)

جغرافیا (3)

شیمی (3)

سلامت و بهداشت

زیست شناسی (3)

اصول عقاید (3)

احکام (3)

تاریخ (3) معارف

تاریخ (3) معارف

ریاضی و آمار (3)

ریاضی و آمار (3)

زبان انگلیسی (3)

زبان انگلیسی (3)

هویت اجتماعی

فلسفه (2)

تاریخ (3)

فارسی (3)

ریاضیات گسسته

هندسه (3)

فیزیک (3) تجربی

فیزیک (3) تجربی

عربی (3)

عربی (3)

ریاضی (3)

سوپراستار

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

72 صفحه

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

8 صفحه

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

کلاس دوازدهمی‌ها

آزمون تستی حسابان (2) دوازدهم دبیرستان شاهد ملایر | فصل 2: مثلثات

1 صفحه

آزمون تستی حسابان (2) دوازدهم دبیرستان شاهد ملایر | فصل 2: مثلثات

سعید ابراهیمی

امتحان ترم اول حسابان دوازدهم دبیرستان امام رضا واحد 1 مشهد | دی 98

2 صفحه

امتحان ترم اول حسابان دوازدهم دبیرستان امام رضا واحد 1 مشهد | دی 98

کلاس دوازدهمی‌ها

نمونه سوال امتحان نوبت اول حسابان (2) دوازدهم رشته ریاضی | سری 1 + پاسخ

2 صفحه

نمونه سوال امتحان نوبت اول حسابان (2) دوازدهم رشته ریاضی | سری 1 + پاسخ

کلاس دوازدهمی‌ها

آزمون مستمر ترم اول حسابان 2؛ فصل 1 و 2

4 صفحه

آزمون مستمر ترم اول حسابان 2؛ فصل 1 و 2

اردوان مختاری

رایـــــگان

راهنمای گام به گام حسابان (2) پایه دوازدهم رشته ریاضی | فصل اول: تابع

25 صفحه

راهنمای گام به گام حسابان (2) پایه دوازدهم رشته ریاضی | فصل اول: تابع

درف شیان

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم | فصل 5: کاربردهای مشتق

21 صفحه

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم |…

علی فقیهی

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم | فصل 2: مثلثات

15 صفحه

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم |…

علی فقیهی

رایـــــگان

سؤالات امتحان نهایی درس حسابان (2) دوازدهم رشته علوم ریاضی | نوبت شهریور 1401

5 صفحه

سؤالات امتحان نهایی درس حسابان (2) دوازدهم رشته علوم ریاضی | نوبت شهریور…

امتحان نهایی

موارد بیشتر

موارد بیشتر

ارسال فایل

رابطه‌ای بنویسید که محیط یک مربع را به صورت تابعی از مساحت آن نمایش دهد.

معادله 2cos²5x-cos5x–3=0 را حل کنید.

تابعی که مساحت مربع را به محیط آن وابسته می‌کند؟

موارد بیشتر

ارسال پرسش

موارد بیشتر