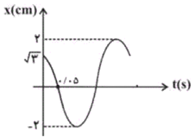
ابتدا با توجه به مکان نوسانگر در لحظه‌ی $t=0$، فاز اولیه‌ی نوسانگر را حساب می‌کنیم. سپس دوره‌ی نوسان را به‌دست می‌آوریم:

$\left\{ \begin{matrix} A=2cm  \\ {{x}_{{}^\circ }}=\sqrt{3}cm  \\ \end{matrix} \right.\Rightarrow x=A\sin (\omega t+{{\varphi }_{{}^\circ }})\xrightarrow{t=0}\sqrt{3}=2\sin (\omega \times 0+{{\varphi }_{{}^\circ }})$

$\Rightarrow \sin {{\varphi }_{{}^\circ }}=\frac{\sqrt{3}}{2}\Rightarrow {{\varphi }_{{}^\circ }}=\frac{\pi }{3}rad$

با توجه به نمودار، پس از لحظه‌ی $t=0$، نوسانگر به طرف مرکز نوسان در حال حرکت است پس در ناحیه‌ی دوم دایره‌ی مرجع قرار دارد و ${{\varphi }_{{}^\circ }}=\frac{2\pi }{3}rad$ قابل قبول است. در ضمن در لحظه‌ی $t=0/05s$، مکان نوسانگر برای اولین بار برابر صفر شده است، بنابراین در این لحظه فاز حرکت باید برابر $\pi $ رادیان باشد، پس به‌ازای $t=0/05s$ و $x=0$ در معادله‌ی نوسانگر داریم:

$0=2\sin (\frac{2\pi }{T}\times 0/05+\frac{2\pi }{3})\Rightarrow \frac{\pi }{10T}+\frac{2\pi }{3}=\pi \Rightarrow T=0/3s$