تقعر تابع به معادلهٔ در کدام بازه رو به پایین است؟ | حسابان (2) دوازدهم شماره 84901

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

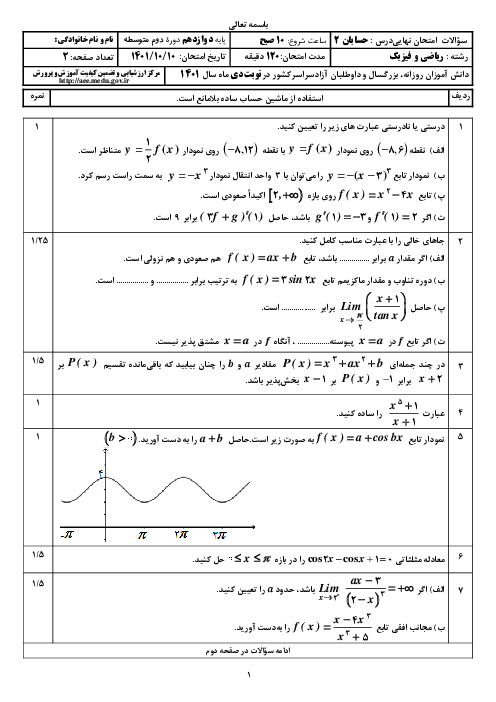
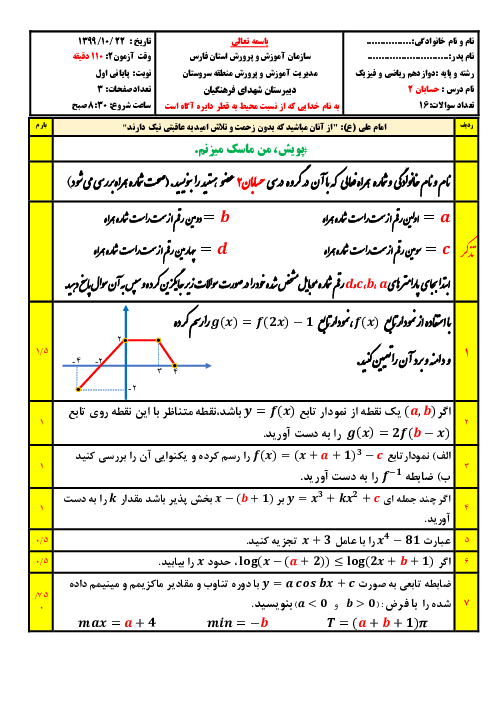
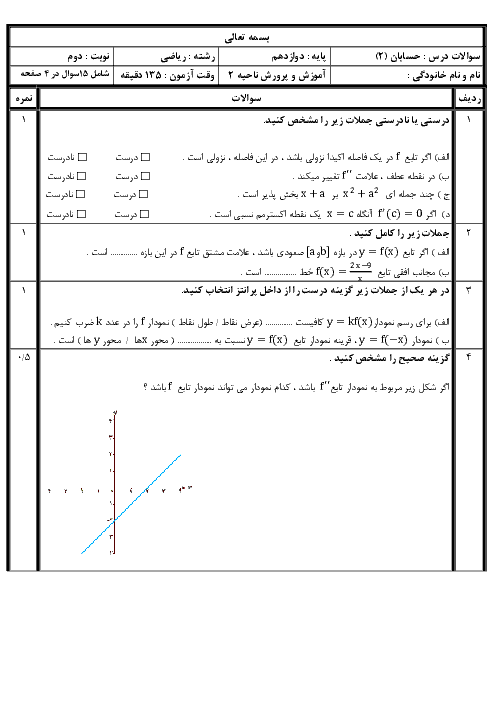
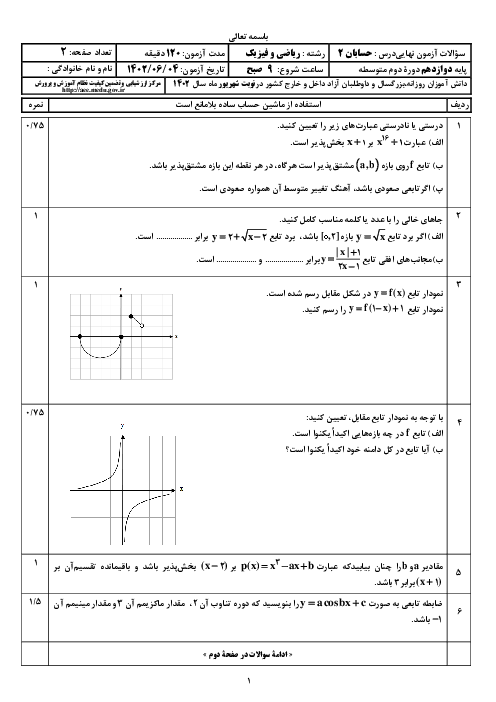
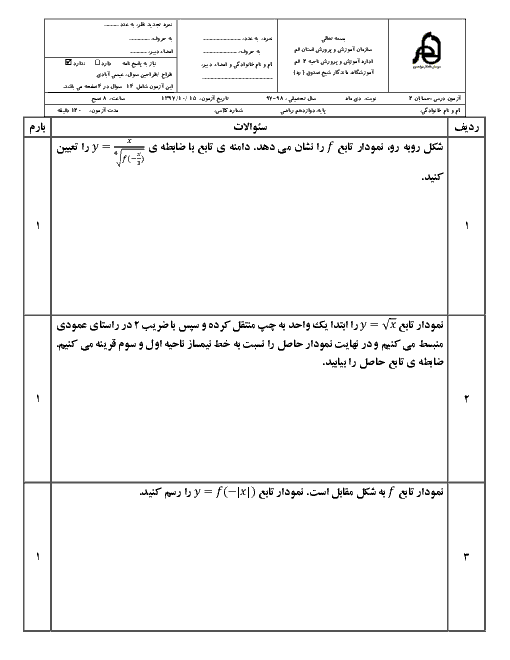
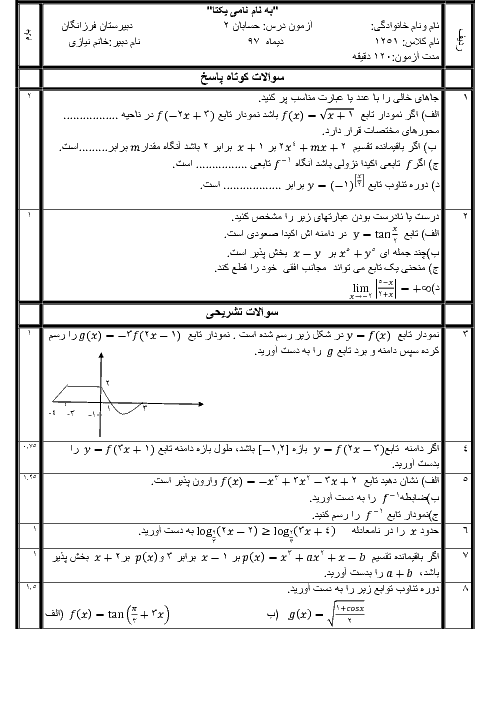
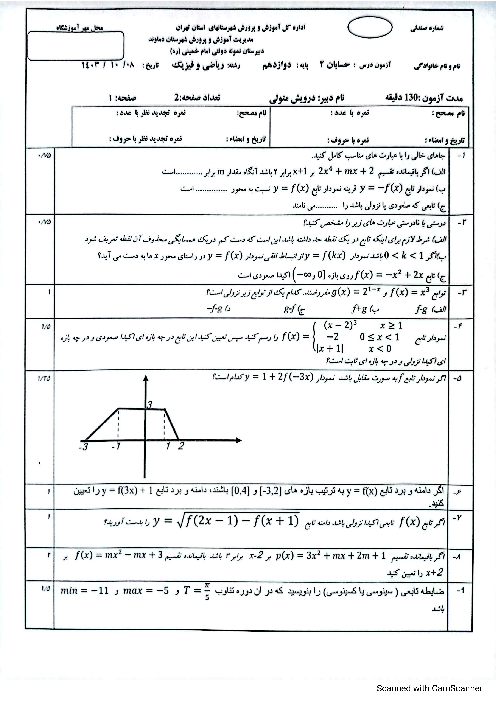
درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

تقعر تابع به معادلهٔ $y={{x}^{2}}+\sqrt{x}$ در کدام بازه رو به پایین است؟

1 )

$\left( 0,\frac{1}{4} \right)$

2 )

$\left( 0,\frac{1}{2} \right)$

3 )

$(0,1)$

4 )

$\left( \frac{1}{4},\frac{1}{2} \right)$

نمایش پاسخ

باید بازه‌ای را بیابیم که آن $y''$ منفی باشد، دامنهٔ تعریف تابع بازهٔ $\left[ 0,+\infty \right)$ است، لذا:

$\begin{align} & y'=2x+\frac{1}{2\sqrt{x}}=2x+\frac{1}{2}{{x}^{\frac{-1}{2}}} \\ & y''=2-\frac{1}{4}{{x}^{\frac{-3}{2}}}=2-\frac{1}{4x\sqrt{x}} \\ \end{align}$

$y''=\frac{8x\sqrt{x}-1}{4x\sqrt{x}}\Rightarrow \left\{ \begin{align} & y''=0\to x\sqrt{x}=\frac{1}{8}\Rightarrow x=\frac{1}{4} \\ & x=0\to (reshey\,makhraj)\,\to y'' \\ \end{align} \right.$

پس در بازهٔ $(0,\frac{1}{4})$، تقعر تابع رو به پایین است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده