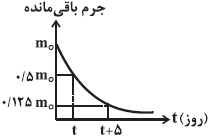
با استفاده از رابطه‌ی ماده‌ی پرتوزای باقی‌مانده، می‌توان نوشت:

$m={{m}_{{}^\circ }}\left( \frac{1}{2} \right)\Rightarrow \frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{2}^{{{n}_{2}}}}}{{{2}^{{{n}_{1}}}}}\xrightarrow[{{m}_{2}}=0/125{{m}_{{}^\circ }}]{{{m}_{1}}=0/5{{m}_{{}^\circ }}}\frac{0/5{{m}_{{}^\circ }}}{0/125{{m}_{{}^\circ }}}={{2}^{{{n}_{2}}-{{n}_{1}}}}$

$\Rightarrow 4={{2}^{{{n}_{2}}-{{n}_{1}}}}\xrightarrow{n=\frac{t}{{{T}_{\frac{1}{2}}}}}\frac{{{t}_{2}}}{{{T}_{\frac{1}{2}}}}-\frac{{{t}_{1}}}{{{T}_{\frac{1}{2}}}}=2\Rightarrow \frac{t+5}{{{T}_{\frac{1}{2}}}}-\frac{t}{{{T}_{\frac{1}{2}}}}=2\Rightarrow {{T}_{\frac{1}{2}}}=2/5$ روز

حال مقدار نیمه‌عمر را در یک رابطه جایگذاری می‌کنیم:

${{m}_{1}}={{m}_{{}^\circ }}{{\left( \frac{1}{2} \right)}^{{{n}_{1}}}}\Rightarrow 0/5{{m}_{{}^\circ }}={{m}_{{}^\circ }}{{\left( \frac{1}{2} \right)}^{{{n}_{1}}}}\Rightarrow {{n}_{1}}=1\Rightarrow \frac{t}{{{T}_{\frac{1}{2}}}}=1\xrightarrow{{{T}_{\frac{1}{2}}}=2/5}t=2/5$ روز