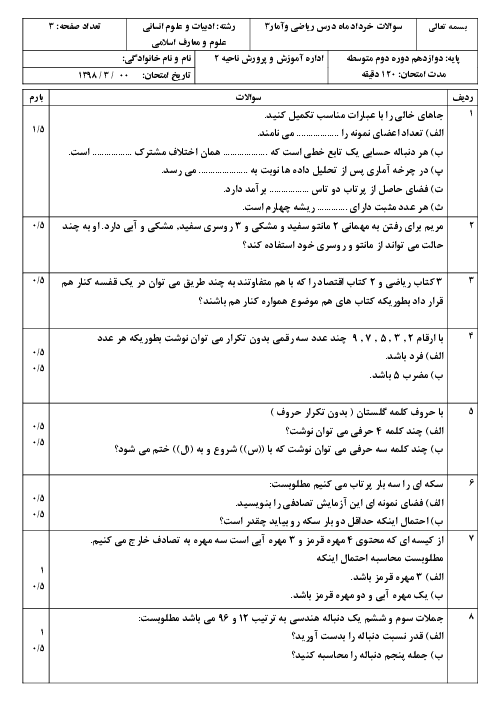
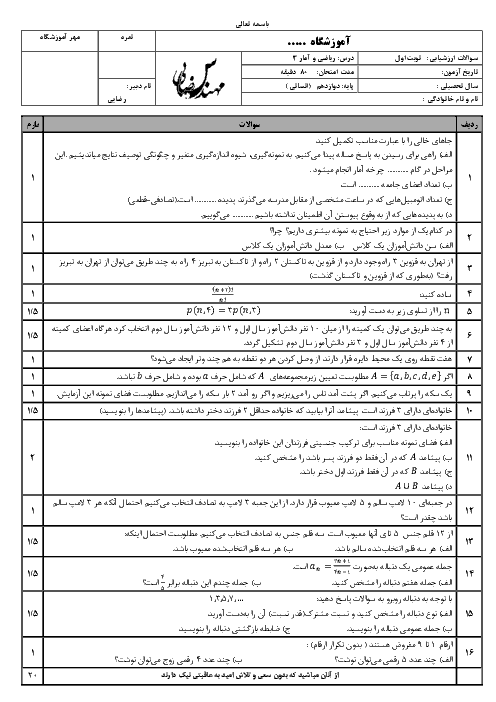
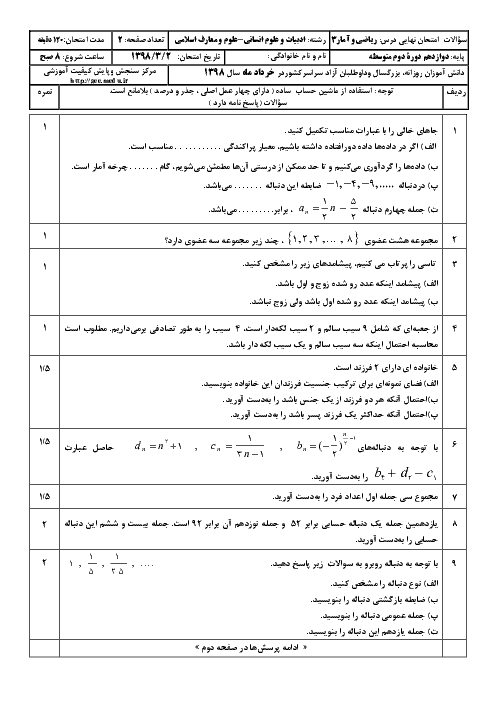
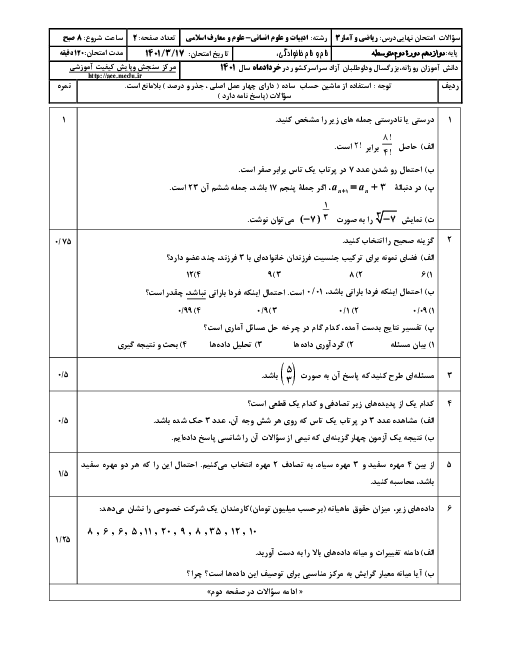
درس 2: ریشه nاُم و توان گویا
ریاضی و آمار (3)
دوازدهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
حاصل عبارت $\frac{8\left( \sqrt{5}-1 \right)}{\sqrt{5}+1}-\frac{\sqrt{5}-2}{\sqrt{5}+2}$ کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!