درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
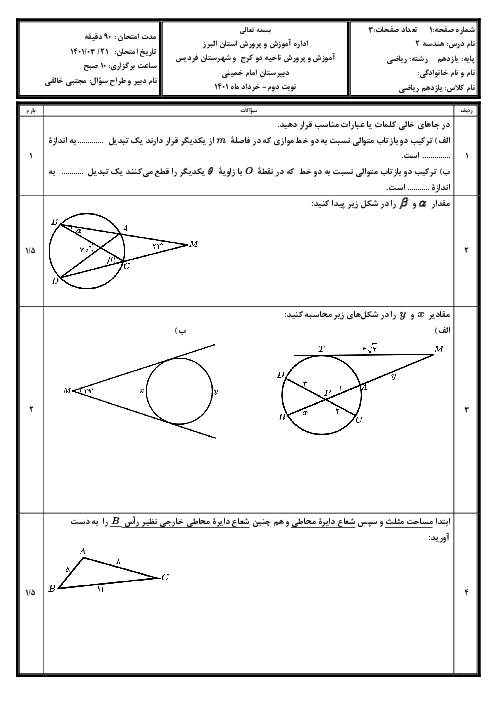
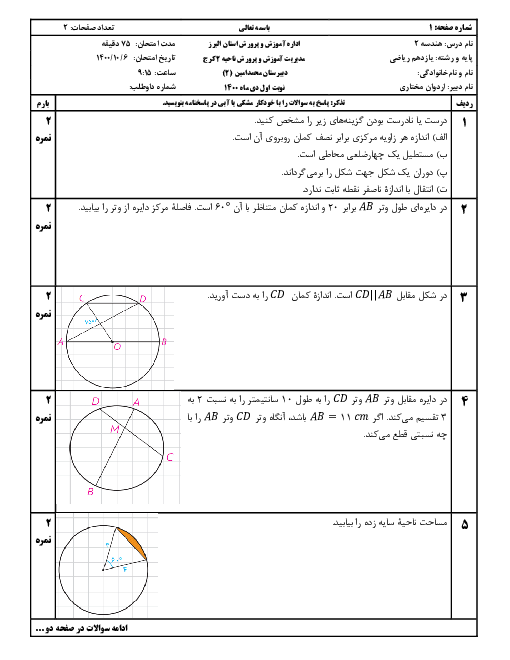
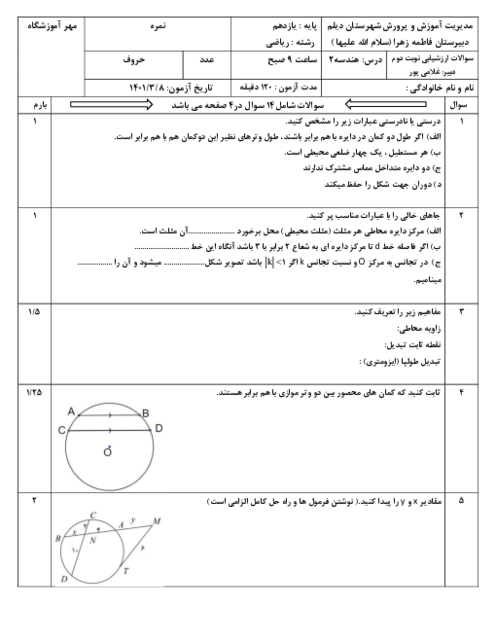
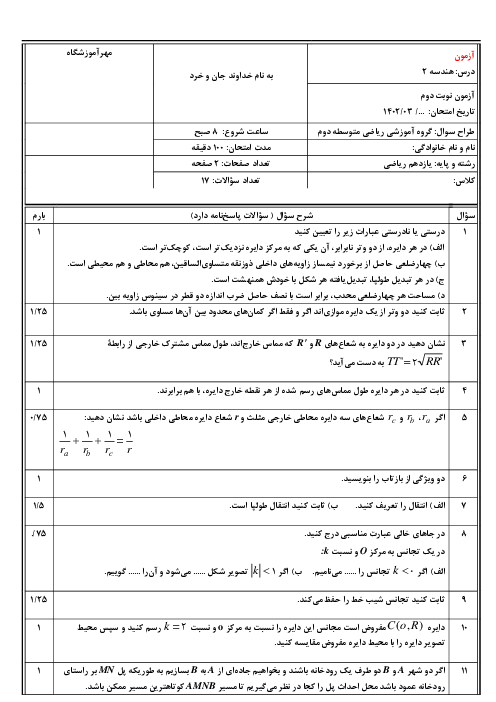
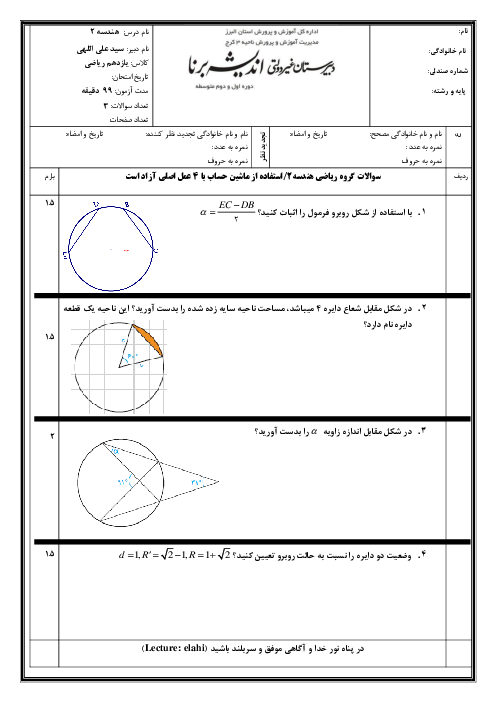
در يک ذوزنقهٔ متساوی‌الساقين، اندازهٔ يكی از زاويه‌ها برابر 60 درجه است. نسبت اندازهٔ شعاع دايرهٔ محيطی به شعاع دايرهٔ محاطی چهارضلعی حاصل از برخورد نيمسازهای داخلی اين ذوزنقه كدام است؟
$\frac{3+\sqrt{3}}{3}$
2 )
$\frac{3-\sqrt{3}}{3}$
3 )
$\frac{3+\sqrt{3}}{2}$
4 )
$\frac{3-\sqrt{3}}{2}$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...