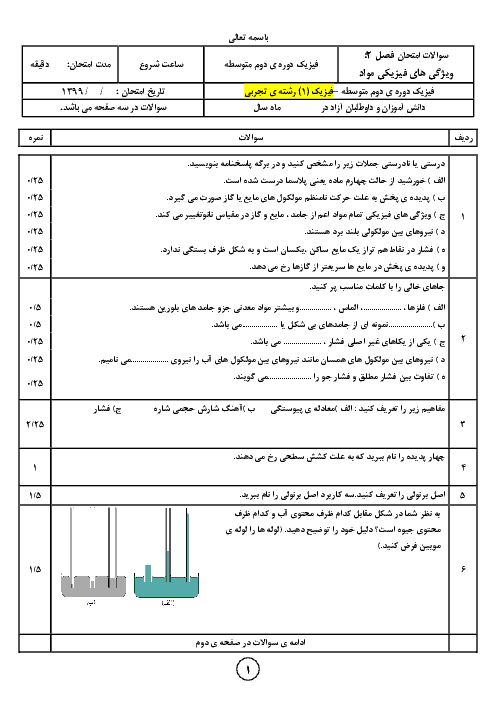
چون در فاصلهٔ 8008 متری بين دو شهر در تابستان تعداد 500 ريل قرار گرفته است، ابتدا طول هر ريل را در دمای ${{40}^{{}^\circ }}C$ به‌دست می‌آوريم و سپس با استفاده از رابطهٔ تغيير طول، حداقل دمای زمستان را حساب می‌كنيم. 

تعداد ریل‌ها $\div $ فاصلهٔ بین شهرها = ${{L}_{2}}$ (${{40}^{{}^\circ }}C$) طول هر ریل در دمای

$\Rightarrow {{L}_{2}}=\frac{8008}{500}\Rightarrow {{L}_{2}}=16/016m$

${{L}_{2}}={{L}_{1}}+{{L}_{1}}\alpha \Delta T\xrightarrow[\alpha =2\times {{10}^{-5}}\frac{1}{K}]{{{L}_{2}}=16/016m,{{L}_{1}}=16m}$

$16/016=16+16\times 2\times {{10}^{-5}}\times \Delta T$

$\Rightarrow 0/016=32\times {{10}^{-5}}\Delta T$

$\Rightarrow \Delta T=\frac{16\times {{10}^{-3}}}{32\times {{10}^{-5}}}\Rightarrow \Delta T=50K={{50}^{{}^\circ }}C$

$\Delta \theta =\Delta T={{\theta }_{2}}-{{\theta }_{1}}\xrightarrow[\Delta T={{50}^{{}^\circ }}C]{{{\theta }_{2}}={{40}^{{}^\circ }}C}50=40-{{\theta }_{1}}=-{{10}^{{}^\circ }}C$