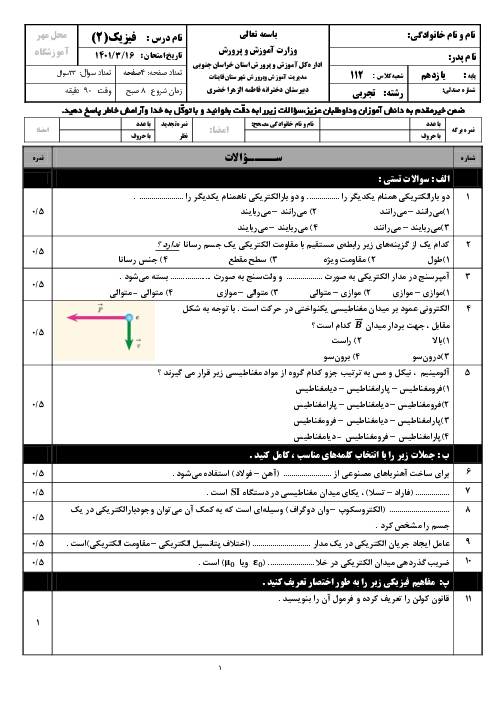
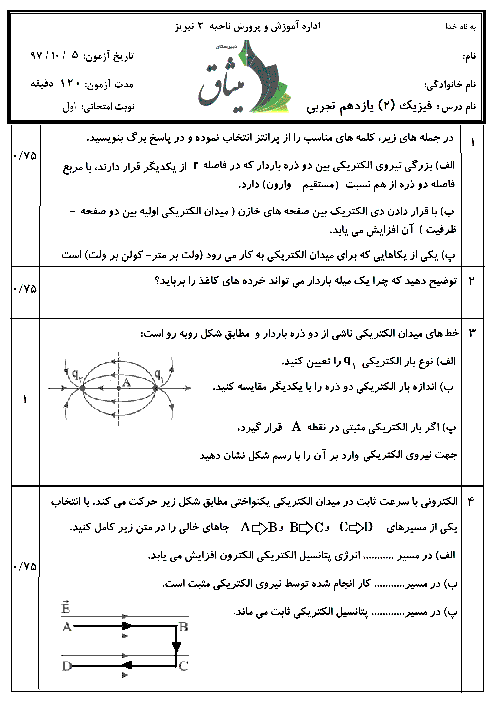
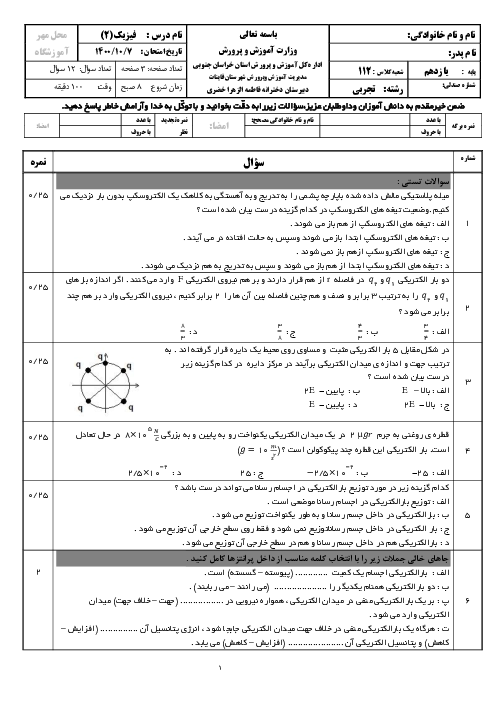
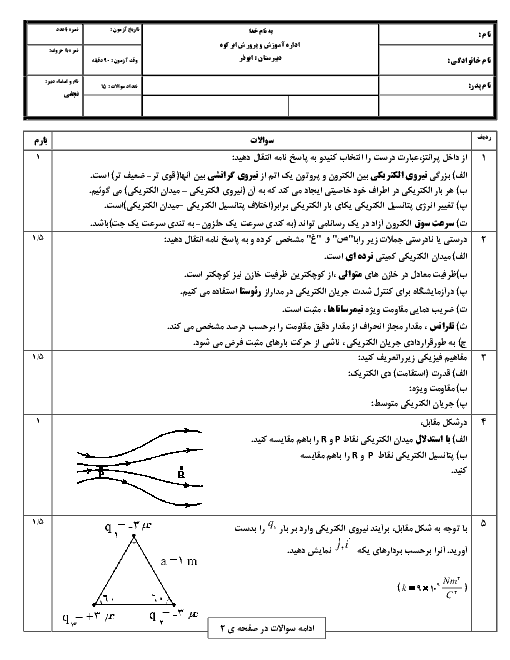
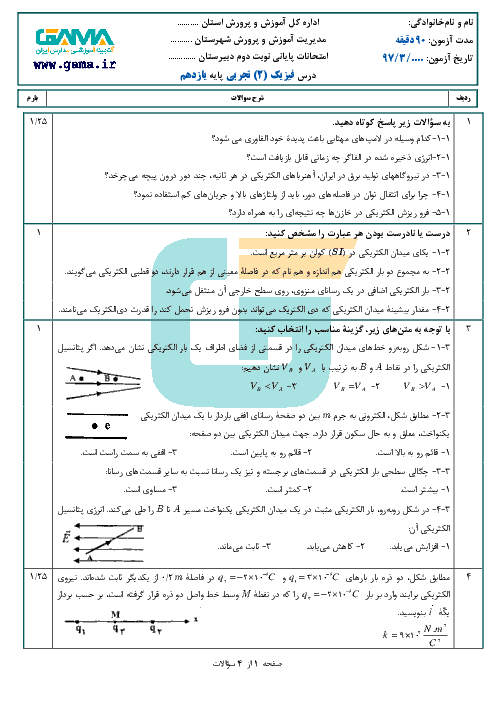
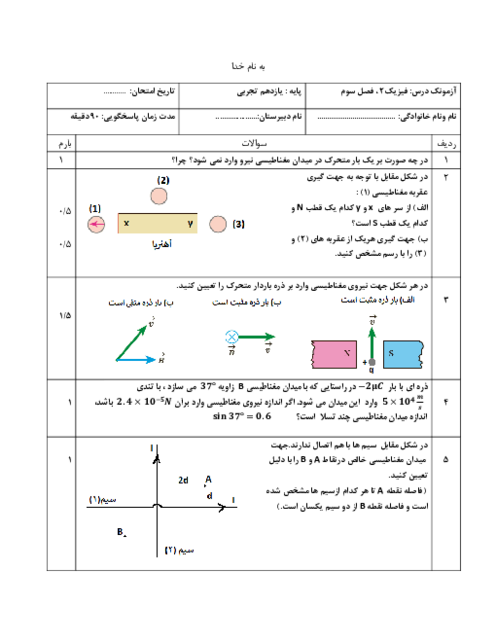
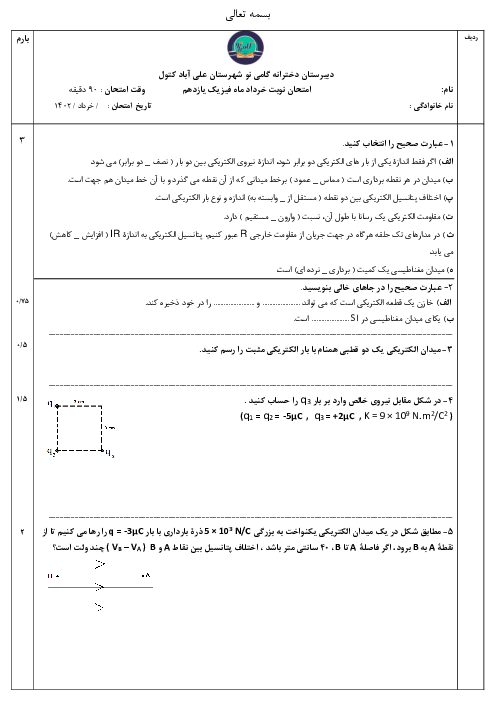
میدان الکتریکی ناشی از بارهای ${{q}_{1}}$ و ${{q}_{2}}$ در نقطهٔ O هماندازه و در خلاف جهت یکدیگر هستند. بنابراین میدان الکتریکی ناشی از این دو بار در نقطهٔ O، یکدیگر را خنثی میکند. برای آنکه میدان الکتریکی کل در نقطهٔ O صفر شود، باید میدان الکتریکی ناشی از بارهای ${{q}_{3}}$ و ${{q}_{4}}$ در نقطهٔ O صفر شود. دقت کنید بار ${{q}_{3}}$ ثابت فرض میشود و مکان جدید بار ${{q}_{4}}$ را بهدست میآوریم.
با توجه به تصویر
${{E}_{3}}={{E}_{4}}\Rightarrow k\frac{\left| {{q}_{3}} \right|}{{{(6)}^{2}}}=k\frac{\left| {{q}_{4}} \right|}{{{(6+x)}^{2}}}\Rightarrow \frac{2}{{{6}^{2}}}=\frac{8}{{{(6+x)}^{2}}}\Rightarrow {{(\frac{6+x}{6})}^{2}}=\frac{8}{2}=4\Rightarrow \frac{6+x}{6}=2\Rightarrow 6+x=12\Rightarrow x=6cm$
بنابراین برای آنکه میدان الکتریکی برایند در نقطهٔ O صفر شود، باید فاصلهٔ بار ${{q}_{4}}$ از بار ${{q}_{3}}$ برابر با $6cm$ باشد. یعنی این بار بهاندازهٔ $8-6=2cm$ به سمت چپ جابهجا شود.